Какие признаки могут быть положены в основание группировки модальный медианный

Обновлено: 02.07.2024

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4 .

Расчёт структурных характеристик вариационного ряда распределения.

- область применения и методику расчёта структурных средних величин;

- исчислять структурные средние величины;

- формулировать вывод по полученным результатам.

В статистике исчисляются мода и медиана, которые относятся к структурным средним, так как их величина зависит от строения статистической совокупности.

Расчёт моды

Модой называется значение признака (варианта), чаще всеговстречающееся в изучаемой совокупности. В дискретном ряду распределения модой будет варианта с наибольшей частотой.

Например : Распределение проданной женской обуви по размерам характеризуется следующим образом:

Количество проданных пар

В этом ряду распределения модой является 37 размер, т.е. Мо=37 размер.

Для интервального ряда распределения мода определяется по формуле:

где Х _Mo - нижняя граница модального интервала;

h_Mo - величина модального интервала;

f_Mo – частота модального интервала;

f_Mo _{- 1 и} f_Mo ₊₁ – частота интервала соответственно

предшествующего модальному и следующего за ним.

Например : Распределение рабочих по стажу работы характеризуется следующими данными.

Стаж работы, лет

Число рабочих, чел.

Определить моду интервального ряда распределения.

Мода интервального ряда составляет

Мода всегда бывает несколько неопределённой, т.к. она зависит от величины групп и точного положения границ групп. Мода широко применяется в коммерческой практике при изучении покупательского спроса, при регистрации цен и т.п.

Расчёт медианы

Медианой в статистике называется варианта, расположенная в середине упорядоченного ряда данных, и которая делит статистическую совокупность на две равные части так, что у одной половины значения меньше медианы, а у другой половины – больше её. Для определения медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания или убывания индивидуальных значений признака.

В дискретном упорядоченном ряду с нечётным числом членов медианой будет варианта, расположенная в центре ряда.

Например : Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7 лет, т.е. Ме=7 лет

Если дискретный упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя арифметическая из двух смежных вариант, стоящих в центре ряда.

Например : Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя арифметическая из этих значений и будет медианой ряда

Чтобы определить медиану для сгруппированных данных, необходимо считать накопленные частоты.

Например: По имеющимся данным определим медиану размера обуви

Количество проданных пар

Сумма накопленных частот

Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину суммы частот ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е. 37 и есть медиана ряда.

Если же сумма накопленных частот против одной из вариант равна точно половине суммы частот ряда, то медиана определяется как средняя арифметическая этой варианты и последующей.

Например : По имеющимся данным определим медиану заработной платы рабочих

Месячная заработная плата, тыс .р уб.

Число рабочих, чел.

Сумма накопленных частот

Медиана будет равна:

Медиана интервального вариационного ряда распределения определяется по формуле:

Где Х_Ме – нижняя граница медианного интервала;

h_Me – величина медианного интервала;

∑ f - сумма частот ряда;

f _Ме – частота медианного интервала;

Например: По имеющимся данным о распределении предприятий по численности промышленно – производственного персонала рассчитать медиану в интервальном вариационном ряду

Группы предприятий по численности ППП, чел.

Сумма накопленных частот

Определим, прежде всего, медианный интервал. В данном примере сумма накопленных частот, превышающих половину суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный интервал, т.е. интервал, в котором находится медиана ряда. Определим её значение

Если же сумма накопленных частот против одного из интервалов равна точно половине суммы частот ряда, то медиана определяется по формуле:

где n – число единиц в совокупности.

Группы предприятий по численности ППП, чел.

Сумма накопленных частот

Моду и медиану в интервальном ряду можно определить графически:

моду в дискретных рядах - по полигону распределения, моду в интервальных рядах - по гистограмме распределения, а медиану - по кумуляте .

Мода интервального ряда распределения определяется по гистограмме распределения определяют следующим образом. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.

Медиана рассчитывается по кумуляте . Для её определения из точки на шкале накопленных частот ( частостей ), соответствующей 50%, проводится прямая , параллельная оси абсцисс, до пересечения с кумулятой . Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

Кроме моды и медианы в вариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения.

Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:

- квартили – значения признака, делящие упорядоченную совокупность на четыре равные части;

- децили – значения признака, делящие упорядоченную совокупность на десять равных частей;

- перцентели - значения признака, делящие упорядоченную совокупность на сто равных частей.

Таким образом, для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значение признака , мода, медиана . При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:

- для устойчивых социально-экономических процессов в качестве показателя центра используют среднюю арифметическую. Такие процессы характеризуются симметричными распределениями, в которых ;

- для неустойчивых процессов положение центра распределения характеризуется с помощью Mo или Me . Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку занимает положение между средней арифметической и модой.

отличие от динамических проявляются только в массовых процессах.

Данная курсовая работа состоит из двух глав: теоретической и расчётной.

В теоретической главе я рассмотрел два вопроса, которые кажутся мне наиболее важными и интересными. В них мы подробно разберем важнейшую часть статистического анализа (а именно построение радов распределения), а также моду и медиану.

Статистические ряды распределения являются одним из наиболее важных элементов статистики. Они представляют собой составную часть метода статистических сводок и группировок, но, по сути, ни одно из статистических исследований невозможно произвести, не представив первоначально полученную в результате статистического наблюдения информацию в виде статистических рядов распределения.

Актуальность данной темы обусловлена тем, что статистические ряды распределения являются базисным методом для любого статистического анализа. Понимание данного метода и навыки его использования необходимы для проведения статистических исследований.

В статистике применяют два вида средних величин, которые определяются только структурой распределения. Такими величинами являются мода и медиана. Их используют как среднюю характеристику в тех совокупностях, где расчёт средне степенной невозможен или нецелесообразен. Мода – наиболее часто встречающееся значение признака у единиц данной совокупности. Мода применяется при изучении качества продукции, покупательского спроса, конструировании одежды, обуви и т. д.

Медиана – варианта, делящая ранжированный ряд на две равные части.

Вторая глава – расчетная. Она состоит из задач, которые включают в себя большой спектр заданий (расчёта среднего показателя, нахождение моды и медианы, метод постоянной средней и многое другое).

Глава 1.Теоретическая часть.

14.Виды рядов распределения.

14.1. Виды рядов распределения

Важнейшей частью статистического анализа является построение рядов распределения (структурной группировки) с целью выделения характерных свойств и закономерностей изучаемой совокупности. В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают соответственно типы рядов распределения.

Если за основу группировки взят качественный признак, то такой ряд распределения называют атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.).

Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу).

Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд.

14.2. Ранжированный ряд

Ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.

Капитал (тыс. руб.)

Другие формы вариационного ряда - групповые таблицы, составленные по характеру вариации значений изучаемого признака. По характеру вариации различают дискретные (прерывные) и непрерывные признаки.

14.3. Дискретный ряд

Дискретный ряд - это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). К последним можно отнести тарифный разряд, количество детей в семье, число работников на предприятии и т.д. Эти признаки могут принимать только конечное число определенных значений.

Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака.

Кол-во детей в семье

14.4. Интервальный вариационный ряд

Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд.

Размер собственного капитала (тыс.руб.)

При построении интервального вариационного ряда необходимо выбрать

оптимальное количество групп, самый распространенный способ по формуле

k 1 + 3,32 lg n= 1 + 1,44 ln n,

где k — число групп;

n — численность совокупности.

14.5. Частота повторения

Частота (частота повторения) - число повторений отдельного варианта значений признака, обозначается f_i , а сумма частот, равная объему исследуемой совокупности, обозначается

где k - число вариантов значений признака

Очень часто таблица дополняется графой, в которой подсчитываются накопленные частоты S, которые показывают, какое количество единиц совокупности имеет значение признака не большее, чем данное значение.

Частоты ряда f могут заменяться частностями w, выраженными в относительных числах (долях или процентах). Они представляют собой отношения частот каждого интервала к их общей сумме, т.е.:

При построении вариационного ряда с интервальными значениями прежде всего необходимо установить величину интервала i, которая определяется как отношение размаха вариации R к числу групп m:

где R = x_max - x_min ; m = 1 + 3,322 lgn (формула Стерджесса); n - общее число единиц совокупности.

24. Мода и медиана

Бесспорно, важное значение имеет такая величина признака, которая встречается в изучаемом ряду, в совокупности чаще всего. Такую величину принято называть модой и обозначать Мо. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных (и даже несколько различных, но больших, чем соседние) значений признака имеются в вариационном ряду, он считается соответственно бимодальным либо мультимодальным. Это говорит о неоднородности совокупности, возможно, представляющей собой агрегат нескольких совокупностей с разными модами.

В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, Т.е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается точечной модой. Логично предположить, что такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Отсюда имеем обычно применяемую формулу :

Мо = хо + f_Mo - fMo - 1 • i,

где хо - нижняя граница модального интервала; fMo - частота в модальном интервале;

fMo - 1 - частота в предыдущем интервале;

fMo + 1 - частота в следующем интервале за модальным; i - величина интервала.

Вычисление моды в интервальном ряду весьма условно.

Приближенно Мо может быть определена графически .

В равно интервальном ряду при расчете моды следует использовать плотность распределения.

К изучению структуры вариационного ряда средняя арифметическая величина тоже имеет отношение, хотя основное значение этого обобщающего показателя другое.

24.2. Медиана.

При изучении вариации применяются такие характеристики вариационного ряда, которые описывают количественно его структуру, строение. Такова, например, медиана - величина варьирующего признака, делящая совокупность на две равные части - со значениями признака меньше медианы и со значениями признака больше медианы. На примере этих данных видно принципиальное различие между медианой и средней величиной. Медиана не зависит от значений признака на краях ранжированного ряда. Если бы капитал крупнейшего банка Санкт-Петербурга был в десять раз больше, величина медианы не изменилась бы. Поэтому часто медиану используют как более надежный показатель типичного значения признака, нежели арифметическая средняя, если ряд значений неоднороден, включает резкие отклонения от средней. В данном ряду средняя величина собственного капитала равна 394 млн руб., сложилась под влиянием наибольшей варианты. 80% банков имеют капитал меньше среднего и лишь 20% - больше. Вряд ли такую среднюю можно считать типичной величиной. При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при 10 значениях признака - среднюю из пятого и шестого значений в ранжированном ряду.

В интервальном вариационном ряду для нахождения медианы применяется формула

Ме = Х_е + fi. L (~ - fMe - 1) ,

Ме где Ме - медиана;

Х_е - нижняя граница интервала, в котором находится медиана;

п - число наблюдений; .

!Ме -\ - накопленная частота в интервале, предшествующем медиан-

fMe - частота в медианном интервале; j - величина интервала.

Например, если имеется 100 наблюдений, то медианными,

Т.е. стоящими в середине ряда, являются: 100,,+ 1 = 50,5 - 50-я

и 51-я единицы. В нашем примере имеется нечетное число значений: 143_+1 = 72, Т.е. в середине ряда находится 72-е от

начала ряда значение урожайности. Как видно из ряда накопленных частот , оно находится в четвертом интервале. Тогда

Ме = 25 + 724135 . 5 = 29,5 цjгa.

При нечетном числе единиц совокупности номер медианы, как видим, равен не 'Lfj: 2, а ('Lfj + 1) : 2, но это различие несущественно и обычно игнорируется на практике.

В равно интервальном ряду медиана - это середина среднего интервала при их нечетном числе или средняя арифметическая из границ двух средних интервалов при их четном числе.

В дискретном вариационном ряду медианой следует считать значение признака в той группе, в которой накопленная частота превышает половину численности совокупности. Например, для данных табл. 5.1 медианой числа забитых за игру мячей будет два.

24.3. Соотношение между средней величиной, медианой и модой.

Различие между средней арифметической величиной, медианой и модой в данном распределении невелико. Если распределение по форме близко к нормальному закону, то медиана находится между модой и средней величиной, причем ближе к средней, чем к моде.

При правосторонней асимметрии х > Ме > Мо; при левосторонней асимметрии х n -1 √X₁ *X₂ *…*X_n

X = 4 √(24/3)(60/24)(120/60)(156/120) = 4 √52 ~ 2,68

Проверка: 4*2,68*2,68*2,68*2,68 ~ 206 => средний коэффициент роста не равен 2,68.

2.6 Задача №6

Определить Моду и Медиану для распределения рабочих сдельщиков по нормам выработки.

Мода на экране, медиана в треугольнике, а средние – это температура по больнице и в палате. Продолжаем наш практический курс занимательной статистики (Занятие 1) изучением центральных характеристик статистической совокупности, названия которых вы видите в заголовке. И начнём мы с его конца, поскольку о средних величинах речь зашла практически с первых же абзацев темы. Для подготовленных читателей оглавление:

Генеральная и выборочная средняя – вычисление по первичным данным и для сформированного дискретного вариационного ряда;
Мода – определение и нахождение для дискретного случая;
Медиана – общее определение, как найти медиану;
Средняя, мода и медиана интервального вариационного ряда – вычисление по первичным данным и по готовому ряду. Формулы моды и медианы, – коротко о главном.

Итак, пусть исследуется некоторая генеральная совокупность объёма , а именно её числовая характеристика , не важно, дискретная или непрерывная (Занятия 2, 3).

Генеральной средней называется среднее арифметическое всех значений этой совокупности:

Если среди чисел есть одинаковые (что характерно для дискретного ряда), то формулу можно записать в более компактном виде:
, где
варианта повторяется раз;
варианта – раз;
варианта – раз;
…
варианта – раз.

Живой пример вычисления генеральной средней встретился в Примере 2, но чтобы не занудничать, я даже не буду напоминать его содержание.

Далее. Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема , и на основании исследования этой выборки делают вывод обо всей совокупности.

Выборочной средней называется среднее арифметическое всех значений выборки:

и при наличии одинаковых вариант формула запишется компактнее:
– как сумма произведений вариант на соответствующие частоты , делённая на объём совокупности.

Выборочная средняя позволяет достаточно точно оценить истинное значение , чего вполне достаточно для многих исследований. При этом, чем больше выборка, тем точнее будет эта оценка.

Практику начнём, а точнее продолжим, с дискретного вариационного ряда и знакомого условия:

По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.

Это числа из Примера 4 (см. по ссылке выше), но теперь нам требуется: вычислить выборочную среднюю, и, не отходя от станка, найти моду и медиану.

Как решать задачу? Если нам даны первичные данные (исходные необработанные значения), то их можно тупо просуммировать и разделить результат на объём выборки:
– среднестатистический квалификационный разряд рабочих цеха.

Далее. Мода и медиана. Эти понятия тоже вводятся как для генеральной, так и для выборочной совокупности, и определения я сформулирую в общем виде.

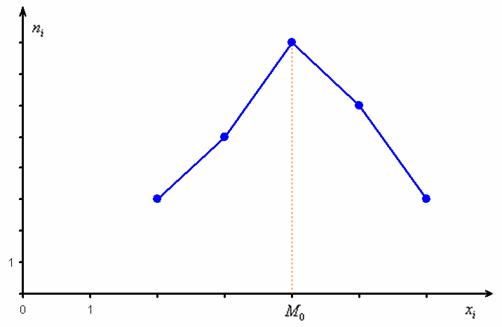
Мода. Мода дискретного вариационного ряда – это варианта с максимальной частотой. В данном случае . Моду легко отыскать по таблице, и ещё легче на полигоне частот – это абсцисса самой высокой точки:

Иногда таковых значений несколько (с одинаковой максимальной частотой), и тогда модой считают каждое из них.

Если все или почти все варианты различны (что характерно для интервального ряда), то модальное значение определяется несколько другим способом, о котором во 2-й части урока.

Медиана. Медиана вариационного ряда* – это значение, которая делит его на две равные части (по количеству вариант).

* не важно, дискретного или интервального, генеральной совокупности или выборочной.

Медиану можно отыскать несколькими способами.

Если даны первичные данные, то сортируем их по возрастанию либо убыванию (см. Задание 1) и находим середину ранжированного ряда: . Почему именно 13-е число? Потому что перед ним находится 12 чисел и после него тоже 12 чисел, таким образом, значение разделило ряд на две равные части, а значит, является медианой. Этот номер можно найти аналитически:

– если совокупность содержит нечётное количество чисел (наш случай), то делим её объём пополам: и округляем полученное значение в бОльшую сторону: 13 – получая тем самым срединный номер.

– если совокупность содержит чётное количество чисел, например, 20, то делаем то же самое: , и медианное значение здесь рассчитывается как среднее арифметическое 10-го и следующего числа: .

Напоминаю, что изложенная инструкция работает для упорядоченного (по возрастанию либо убыванию) ряда. Но есть и более быстрый путь, где ничего не нужно сортировать. Это использование стандартной функции Экселя:

– забиваем в любую свободную ячейку =МЕДИАНА(, выделяем мышью все числа, закрываем скобку ) и жмём Enter. Попробуйте самостоятельно. Этот способ удобен, когда вам дано много значений.

Следует отметить, что в Экселе существуют и отдельные функции для вычисления средней (=СРЗНАЧ), моды (=МОДА) и ещё много чего, но я против использования этих функций в учебном курсе, за исключением случаев, где это действительно целесообразно. …Почему против? Потому что они не помогают понять суть показателей и, более того, отупляют. Так, среднюю гораздо вразумительнее рассчитывать следующим образом:

=СУММ(выделяем мышью диапазон) / объем совокупности. Вычисления рекомендую опробовать лично (ссылка выше).

Запишем красивый ответ:

Полученные значения близки друг к другу, и это говорит о симметрии вариационного ряда относительно центра, что хорошо видно по полигону частот (см. чертёж выше). И с высокой вероятностью можно утверждать, что примерно так же распределена и вся генеральная совокупность (все рабочие цеха).

И тут возникает следующий закономерный вопрос: а зачем вообще нужна мода с медианой? – ведь есть средняя.

А дело в том, что в ряде случаев среднее значение неудовлетворительно характеризует центральную тенденцию статистической совокупности:

…ну, а если вам не нравятся пиджаки, то представьте какие-нибудь шляпки с цветочками :)

Также обратим внимание, что в условии задачи ничего не сказано о том, генеральная ли это совокупность или выборочная, и в подобной ситуации я не рекомендую ничего додумывать – среднюю просто обозначаем через , без подстрочного индекса.

Вычислить среднюю – в экселевском файле уже забиты исходные данные и приведена краткая инструкция. Если под пальцами нет Экселя, то считаем на калькуляторе. Не ленимся! – заданий я предлагаю немного (у вас своих хватает :)), но прорешать их очень важно! Краткое решение для сверки в конце урока.

…какие мысли на счёт полученного значения ? С такой статистикой магазин разорится.

И, конечно, важнейший показатель здесь мода: . Потому что такая мода :) Более того, в прикладных исследованиях рассматривают несколько модальных значений (вроде даже в Экселе функция есть), в частности, ещё одной модой можно считать варианту . Но это уже попсовая статистика, которую я не буду развивать в этом курсе.

Что будет, если к совокупности добавить руководящий персонал и директора Петрова? Средняя зарплата немного увеличится: , и это уже будет несколько искажённая картина.

А вот если сюда добавить олигарха Петровского, то полученная средняя вообще вызовет широкое возмущение общественности.

Как вычислить моду, медиану и среднюю интервального ряда?

Начнём опять с ситуации, когда нам даны первичные статические данные:

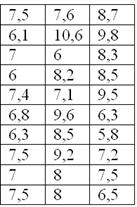
По результатам выборочного исследования цен на ботинки в магазинах города получены следующие данные (ден. ед.):

– это в точности числа из Примера 6 статьи об интервальном вариационном ряде.

Но теперь нам нужно найти среднюю, моду и медиану.

Решение: чтобы найти среднюю по первичным данным, нужно просуммировать все варианты и разделить полученный результат на объём совокупности:
ден. ед.

Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то, конечно, забиваем в любую свободную ячейку =СУММ(, выделяем мышкой все числа, закрываем скобку ), ставим знак деления /, вводим число 30 и жмём Enter. Готово.

Что касается моды, то её оценка по исходным данным, становится непригодна. Хоть мы и видим среди чисел одинаковые, но среди них запросто может найтись пять так шесть-семь вариант с одинаковой максимальной частотой, например, частотой 2. Кроме того, цены могут быть округлёнными. Поэтому модальное значение рассчитывается по сформированному интервальному ряду (о чём чуть позже).

Чего не скажешь о медиане: забиваем в Эксель =МЕДИАНА(, выделяем мышью все числа, закрываем скобку ) и жмём Enter: . Причём, здесь даже ничего не нужно сортировать.

Но в Примере 6 была проведена сортировка по возрастанию (вспоминаем и сортируем – ссылка выше), и это хорошая возможность повторить формальный алгоритм отыскания медианы. Делим объём выборки пополам:

, и поскольку она состоит из чётного количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного ряда:

Ситуация вторая. Когда дан готовый интервальный ряд (типичная учебная задача).

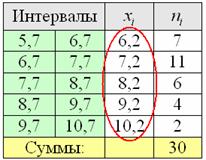
Продолжаем анализировать тот же пример с ботинками, где по исходным данным был составлен ИВР. Для вычисления средней потребуются середины интервалов:

– чтобы воспользоваться знакомой формулой дискретного случая:

– отличный результат! Расхождение с более точным значением (), вычисленным по первичным данным, составляет всего 0,04.

Здесь мы использовали упомянутый ранее приём – приблизили интервальный ряд дискретным, и это приближение оказалось весьма эффективным. Впрочем, особой выгоды тут нет, т.к. при современном программном обеспечении не составляет труда вычислить точное значение даже по очень большому массиву первичных данных. Но это при условии, что они нам известны ;)

С другими центральными показателями всё занятнее.

Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в данной задаче это интервал с частотой 11, и воспользоваться следующей страшненькой формулой:
, где:

– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предыдущего интервала;
– частота следующего интервала.

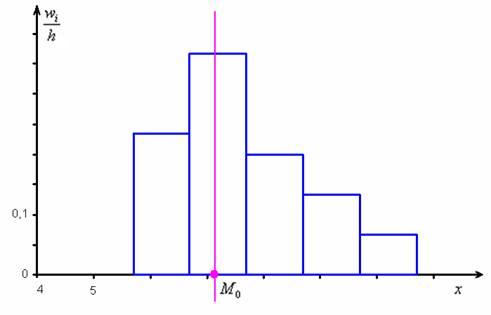
Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот и отмечу :

откуда хорошо видно, что мода смещена относительно центра модального интервала в сторону левого интервала с бОльшей частотой. Логично.

Справочно разберу редкие случаи:

– если модальный интервал крайний, то либо ;

– если обнаружатся 2 модальных интервала, которые находятся рядом, например, и , то рассматриваем модальный интервал , при этом близлежащие интервалы (слева и справа) по возможности тоже укрупняем в 2 раза.

– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым 2 или бОльшее количество мод.

Вот такой вот депеш мод :)

И медиана. Если дан готовый интервальный ряд, то медиана рассчитывается чуть по менее страшной формуле, но сначала нудно (описка по Фрейду:)) найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две равные части.

Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит 30/2 = 15-ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко прийти к выводу, что эти варианты содержатся в интервале .

Формула медианы:
, где:
– объём статистической совокупности;
– нижняя граница медианного интервала;
– длина медианного интервала;
– частота медианного интервала;
– накопленная частота предыдущего интервала.

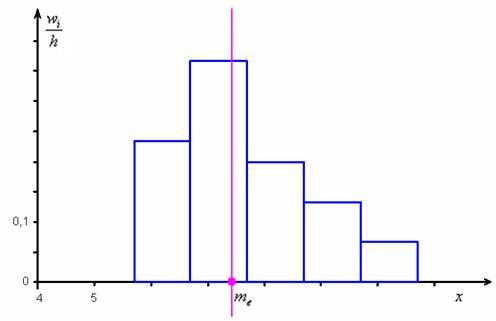
Таким образом:
ден. ед. – заметим, что медианное значение, наоборот, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:

И справочно особые случаи:

– Если медианным является крайний левый интервал, то ;

– Если вариационный ряд содержит чётное количество вариант и две средние варианты попали в разные интервалы, то объединяем эти интервалы, и по возможности удваиваем предыдущий интервал

Ответ: ден. ед.

Здесь центральные показатели оказались заметно отличны друг от друга, и это говорит об асимметрии распределения, которая хорошо видна по гистограмме.

И задача для тренировки:

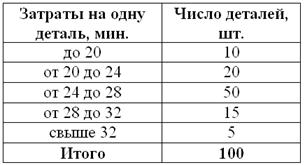
Для изучения затрат времени на изготовление одной детали рабочими завода проведена выборка, в результате которой получено следующее статистическое распределение:

…да, тематичная у меня получилась статья :)

Найти среднюю, моду и медиану.

Решаем эту задачу в Экселе – все числа и инструкции уже там. Если нет Экселя, считаем на калькуляторе, что в данном случае может оказаться даже удобнее. Образец решения, как обычно, в конце урока.

В таких случаях вариационный ряд дробят с помощью квартилей, децилей, а в ~~упоротых~~ специализированных исследованиях – и с помощью перцентилей.

Квартили упорядоченного вариационного ряда – это варианты , которые делят его на 4 равные (по количеству вариант) части. Откуда автоматически следует, что 2-я квартиль – есть в точности медиана: .

В тяжёлых случаях проводится разбиение на 10 частей – децилями – это варианты, который делят упорядоченный вариационный ряд на 10 равных (по количеству вариант) частей.

И в очень тяжелых случаях в ход пускается 99 перцентилей .

И после разбиения вариационного ряда каждый участок исследуется по отдельности – рассчитываются локальные средние показатели, локальные показатели вариации и т.д.

В учебном курсе квартили, децили, перцентили встречаются редко, и посему я оставляю этот материал (их нахождение) для самостоятельного изучения.

Ну а сейчас мы перейдём к рассмотрению другой группы статистических показателей – как раз к показателям вариации.

Решения и ответы:

Кроме того, медиану легко усмотреть и устно – поскольку половина совокупности равна , а сумма первых двух частот , то совершенно понятно, что 250-й и 251-й пиджак – двухпуговичные.

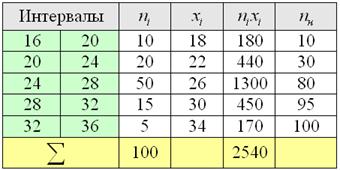
Пример 11. Решение: поскольку длина внутренних интервалов равна , то длины крайних интервалов полагаем такими же (см. конец статьи Интервальный вариационный ряд). Заполним расчётную таблицу:

Вычислим выборочную среднюю:
мин.

Моду вычислим по формуле , в данном случае:
– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предшествующего интервала;
– частота следующего интервала.
Таким образом:
мин.

Анализируя накопленные частоты, приходим к выводу, что медианным является интервал (именно он содержит 50-ю и 51-ю варианты, которые делят ряд пополам).
Медиану вычислим по формуле , в данном случае:
– нижняя граница медианного интервала;
– длина этого интервала;
– объём статистической совокупности;
– частота медианного интервала;
– накопленная частота предыдущего интервала.
Таким образом:
мин.

Ответ: среднее время изготовления детали характеризуется следующими центральными характеристиками:

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Для получения более полной характеристики случайных величин кроме средней величины рассчитываются так называемые структурные средние. К ним относят моду и медиану. Данная статья представляет собой результаты исследовательского проекта.

Мода — это наиболее встречающееся значение признака, или, иначе говоря, значение признака, имеющее наибольшую повторяемость (частоту). Моду рассчитывают по-разному, в зависимости от того, как изменяется случайная величина — дискретно или непрерывно.

где — нижняя граница модального интервала;

— величина интервала;

— частота модального интервала;

— частота интервала, предшествующего модальному;

— частота интервала, следующего за модальным.

Определить модальное значение признака можно и по графику. Для этого в случае дискретно изменяющихся случайных величин строится полигон распределения. На оси абсцисс откладываются значения признака, а на оси ординат — соответствующие им частоты. Значение абсциссы, соответствующие наибольшей вершине полигона, будет значением моды.

Для определения моды в случае непрерывно изменяющейся случайной величины строится гистограмма. В этом случае на оси абсцисс находятся значения границ интервалов значений случайной величины, а на оси ординат — соответствующие этим интервалам частоты. На гистограмме модальному интервалу будет соответствовать столбец, имеющий наибольшую высоту. Затем необходимо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускают перпендикуляр. Абсцисса этой точки и будет модой.

Ряд распределения случайной величины может содержать несколько модальных значений: имеющий одну моду, называется унимодальным, две — бимодальным, три и более — мультимодальным.

Медиана — это значение признака, которое делит все данные на две равные части: половина единиц совокупности имеет значения признака не меньше медианы, другая половина — значения признака не больше медианы.

В случае непрерывно изменяющихся случайных величин сначала определяют медианный интервал. Для этого рассчитывают порядковый номер медианы . Накопленной частоте, присущей медиане (номеру медианного значения признака) соответствует медианный интервал. Обозначим накопленную частоту как . Непосредственно расчет медианы в медианном интервале проводят по формуле:

где - нижняя граница медианного интервала;

- величина медианного интервала

- накопленная частота интервала, предшествующего медианному;

частота медианного интервала.

Медиана может быть определена графически по кумуляте. Для этих целей на оси ординат, где отмечаются накопленные частоты, находится точка, соответствующая полусумме всех частот, т. е. порядковому номеру медианы. Из нее проводится прямая параллельно оси абсцисс до пересечения с графиком. Абсцисса точки пересечения и соответствует медиане.

Для определения медианы в случае дискретно изменяющихся случайных величин значения изучаемого признака ранжируют, т. е. располагают в порядке возрастания (или убывания). Если число единиц совокупности нечетное, то значение признака, находящееся в середине ранжированного ряда, будет являться медианой. Если число единиц будет четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.

В качестве практического примера рассмотрим результаты сдачи ЕГЭ по математике некоторой совокупностью учащихся в количестве 170 человек. При этом с некоторым допущением будем считать результат сдачи ЕГЭ непрерывно изменяющейся величиной, т. е. применим соответствующую формулу расчета. Данные представлены в таблице 1.

Данные о результатах сдачи ЕГЭ по математике по 100-бальной шкале

Величина балла по 100-бальной шкале (x_i)

Количество учащихся (f_i)

Читайте также: