Согласно каким правилам можно осуществлять сложение векторов

Обновлено: 19.05.2024

$\overrightarrow a (a_1 ;a_2 ) + \overrightarrow b (b_1 ;b_2 ) = \overrightarrow c (a_1 + b_1 ;a_2 + b_2 )$

Свойства сложения векторов:

Для любых векторов

$\overrightarrow a (a_1 ;a_2 ),\overrightarrow b (b_1 ;b_2 ),\overrightarrow c (c_1 ;c_2 )$

$\overrightarrow a + (\overrightarrow b + \overrightarrow c ) = (\overrightarrow a + \overrightarrow b ) + \overrightarrow c ;$

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

$\overrightarrow a + ( - \overrightarrow a ) = \overrightarrow <0.> $

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

$\overrightarrow b (b_1 ;b_2 ) + \overrightarrow a (a_1 ;a_2 ) = (\overrightarrow <b_1 + a_1 ;b_2 + a_2 > ) = (\overrightarrow ).$

Так как соответствующие координаты равны, то эти векторы равны.

$2)\overrightarrow a (a_1 ;a_2 ) + (\overrightarrow b (\overrightarrow <b_1 ;b_2 > ) + \overrightarrow c (c_1 ;c_2 )) =$

$(\overrightarrow a (a_1 ;a_2 ) + \overrightarrow b (\overrightarrow <b_1 ;b_2 > )) + \overrightarrow c (c_1 ;c_2 ) =$

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

$\overrightarrow <AB> + \overrightarrow = \overrightarrow .$

$\overrightarrow <AB> (x_2 - x_1 ;y_2 - y_1 ),$

$\overrightarrow <BC> (x_3 - x_2 ;y_3 - y_2 ),$

$\overrightarrow <AC> (x_3 - x_1 ;y_3 - y_1 ).$

$\overrightarrow <AB> + \overrightarrow = (\overrightarrow ) =$

$= (\overrightarrow <x_3 - x_1 ;y_3 - y_1 > ) = \overrightarrow .$

Что и требовалось доказать.

Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

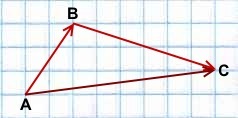
Например,

$\overrightarrow <AB> + \overrightarrow = \overrightarrow$

(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

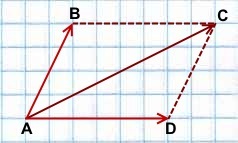
Например,

$\overrightarrow <AB> + \overrightarrow = \overrightarrow$

Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Построить сумму векторов

1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

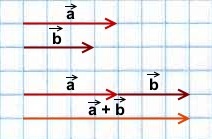
2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

В алгебре часто при упрощении выражений и различных вычислениях используются переместительный и сочетательный законы.

Эти законы также справедливы для векторов.

Вспомним правило сложения векторов – правило треугольника.

Пусть нам даны два вектора а и b.

От произвольно выбранной точки А отложим вектор АВ, равный вектору а.

Затем от точки В отложим вектор ВС, равный вектору b.

Вектор АС называется суммой векторов а и b.

Воспользуемся этим правилом треугольника для доказательства следующей теоремы.

Для любых векторов а , b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а (переместительный закон);

сумма векторов а плюс b и с равна сумме векторов а и b плюс с (сочетательный закон).

Для доказательства переместительного закона рассмотрим случай, когда векторы а и b не коллинеарны, т.е. ненулевые и не лежат на одной или параллельных прямых (случай коллинеарных векторов рассмотрите самостоятельно).

От произвольной точки А отложим вектор АВ, равный вектору а, и вектор АD, равный вектору b.

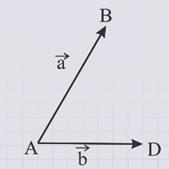
Основываясь на построенных векторах, достроим параллелограмм АВСD так, что вектор АВ равен вектору DС, а вектор АD равен вектору ВС.

По правилу треугольника сумма векторов АВ и ВС равна вектору АС, т.е. равна сумме векторов а и b.

С другой стороны, сумма векторов AD и DC также равна вектору АС, т.е. сумме векторов b и а.

Таким образом, сумма векторов а и b равна сумме векторов b и а.

Переместительный закон доказан.

Для доказательства сочетательного закона отложим от произвольной точки А вектор АВ, равный вектору а, от точки В вектор ВС, равный вектору b, и от точки С вектор CD, равный вектору с.

Рассмотрим сумму векторов а плюс b и вектора с с точки зрения правила треугольника: сумма векторов а и b равна вектору АС, в свою очередь, сумма вектора АС и вектора с равна вектору АD.

Теперь рассмотрим сумму векторов а и b плюс с: сумма векторов b и с, согласно рисунку, равна вектору ВD, в свою очередь, сумма векторов а и ВD равна вектору АD.

Исходя из этого, сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

Что доказывает сочетательный закон.

Важно отметить, что при доказательстве переместительного закона было обосновано правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы а и b, необходимо от произвольной точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b.

Правило треугольника и правило параллелограмма находят сумму двух векторов, но как сложить несколько векторов?

Чтобы сложить несколько векторов, необходимо сложить первый вектор со вторым, затем сложить их сумму с третьим вектором и так далее.

Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке происходит сложение.

Рассмотрим рисунок, отражающий сумму векторов а, b и с:

от произвольной точки А отложен вектор АВ, равный вектору а, затем от точки В отложен вектор ВС, равный вектору b, и, наконец, от точки С отложен вектор CD, равный вектору с.

В результате получается вектор АD, равный сумме векторов а, b и с.

Если продолжить процесс откладывания векторов, можно построить сумму четырех, пяти, любого количества векторов.

Правило построения суммы нескольких векторов называется правилом многоугольника: если А1, А2, …,Аn – произвольные точки плоскости, то сумма векторов А1А2, А2А3, …, Аn –1An равна вектору А1Аn.

Это равенство справедливо для всех точек А1, А2, …, Аn, в частности, когда некоторые из них совпадают.

Важно заметить, что если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.

Итак, подведем итоги:

– Для любых векторов а, b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а;

сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

– Чтобы сложить неколлинеарные векторы а и b, необходимо от точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b (правило параллелограмма).

Читайте также: