Индийские математики представляли себе числа имущества и числа долги как называют такие числа

Обновлено: 05.05.2024

По мнению ученых числа появились еще тогда, когда человеку удалось научиться считать окружающие предметы. Это произошло очень и очень давно. Но знаки, обозначающие числа, появились по меркам истории относительно недавно.

Наука считает, что это произошло в 3000-2000 гг. до н. э. Их изобретение приписывают шумерам – народу, проживавшему на территории Месопотамии (в нынешнее время Ирак).

Историки полагают, что глиняные таблички, на которых они выдавливали определенные черточки, привели к изобретению клинописи. Ею обозначали своеобразные разрядные числа: единицы, десятки, сотни, и также они являлись обозначением цифр. Все остальные записи делались при помощи объединения данных знаков.

Использование цифр существенно упрощало подсчеты: вели счет дням недели, количеству голов скота, объемам урожая, считали размеры участков земли. После шумеров в Месопотамии появились вавилоняне. Они получили систему чисел в наследство от шумеров. До наших дней сохранились таблички-клинопись, на которых изображены превращения шумерских единиц для измерений в вавилонские.

Древние египтяне также использовали цифры. Свидетельством тому является находка Ринда – папирус с математическим трактатом, носящим имя изучавшего Египет англичанина и купившего его в 1858 году в стране пирамид. Такой случай представился в Луксоре. Документ содержит записи 84 математических заданий. Все они с решениями. Глядя на папирус, видно использование в Египте такого порядка цифр, где числовое обозначение – это сумма цифровых значений. При обозначении разрядных чисел, кратных десяти: 1, 10, 100, и т.д., египтяне придумали специальный иероглиф. Записывая разные числа, этот символ использовали такое количество раз, сколько в числе единиц данного разряда.

Похожая система счета существовала у римлян. Ей повезло больше других: она оказалась долгожителем среди древних систем счисления. Иногда ее используют и наши современники.

Такие народы, как финикийцы или древние греки, использовали в качестве цифр буквы.

Распространение индийских числовых обозначений в арабских странах приписывают работам двух математиков. Это Хорезми, живший ок. 780-ок. 850 гг. в Средней Азии и арабский ученый Кинди (ок.800-ок. 870). Первый, в Багдаде написал трактат о цифрах из Индии. Европейскую известность труд получил после перевода математика из Италии Леонардо Пизанского (Фибоначчи). Эта работа привела к закреплению арабо-индийской числовой системы в Европе.

Арифметика каменного века

Обучаться счету наши предки стали на заре своего развития. Учила их этому окружающая жизнь. Охота была главным способом добычи еды. Чтобы не упустить жертву, ее окружали с разных сторон. Пять человек с одной стороны, четыре с другой. Здесь счет выходил на первое место. Люди, даже не имея понятий о цифрах, обходились показом на пальцах. До сих пор существуют племена, пользующиеся таким видом счета.

Археологи, нашедшие поселение древних людей, обнаружили среди волчьих останков кость, с нанесенными отметинами. 55 нанесенных зазубрин указывают на то, что древний охотник вел расчеты при помощи пальцев. Из рисунка на кости можно узнать, что количество зарубок составляет 11 групп по 5 отметин. Начальные 5 групп отделены от других удлиненной отметиной.

Человечество далеко продвинулось вперед с той поры. Но и поныне швейцарские фермеры, отвозя молоко для обработки, зарубками отмечают количество отправляемых емкостей.

Для успешного занятия сельским хозяйством, необходимы были знания арифметики. Не рассчитав количество дней, определить время посева, начало полива составляло определенные трудности. Нужно было определять сроки появления приплода у животных, численность скота в загоне, какое количество урожая помещено в амбары.

Примерно за 6 тыс. лет до н. э. скотоводы того времени начали лепить из глины различные предметы для подсчета животных в стаде. Чтобы узнать, все ли стадо вернулось домой, пастух откладывал в сторону один глиняный кружочек за каждую возвратившуюся овцу. Когда число кружочков и количество животных совпадало, считавший шел отдыхать. Его стадо состояло не только из овец. На пастбища выгоняли коров, коз и других животных. Поэтому возникала потребность в изготовлении и других глиняных фигурок. Люди, обрабатывавшие землю, при помощи таких изделий подсчитывали размеры полученного урожая. Число мешков в амбаре, количество выжатого масла в кувшинах. Сколько у него имеется кусков полотна. Все это требовало подсчета. Когда в стаде случался приплод, хозяин добавлял новые кружочки. При забое скота некоторые фигурки приходилось убирать в сторону.

Так, не зная счета, древние совершали арифметические действия.

Получение названий числами

Прошло немало столетий, или даже тысячелетий, чтобы одинаковые числа стали относиться к различным предметам. В это время и возникли универсальные числовые названия.

Это весьма обширное понятие из математики, с которым школьники сталкиваются уже в 5 классе.

Целые числа — это.

Целые числа – это все положительные, все отрицательные числа и ноль. Главное, чтобы они не содержали дробной части.

Согласно этому определению, к целым числам можно отнести:

-1256, -35, -9, 0, 14, 95, 2020

и так далее. Ведь у них нет дробной части. А вот числа:

0.5, 13.1319, ½, -¾, — 237.3

и так далее не могут считаться целыми, так как у них есть какие-то цифры после запятой или они являются дробью.

Все многообразие целых чисел называется множеством целых чисел. Это официальный математический термин. И обозначается он буквой Z.

В это множество входят и так называемые натуральные числа (это что?). Это все те, которые имеют положительное значение, но опять же без дробной части. Проще говоря, все числа, которые мы используем при счете. Например, 1, 2, 5, 10, 100 и так далее.

Множество натуральных чисел обознается буквой N. И зависимость его и множества целых чисел наглядно показана на следующем рисунке.

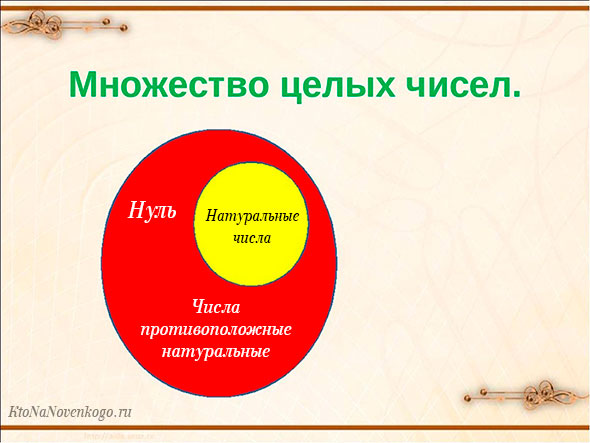
Отсюда можно сделать важный вывод:

Любое натуральное число автоматически является еще и целым. Но при этом далеко не каждое целое число является еще и натуральным.

А можно представить это и в таком варианте. Целые числа — это:

Натуральные числа;
Ноль;
Отрицательные числа.

Каким бы определением вы не пользовались, главное, чтобы было все понятно.

История изучения целых чисел

Опять же эту историю нужно разделить на три части. Ведь изучение натуральных чисел, а также открытие нуля и отрицательных чисел происходило независимо друг от друга. Да еще и в разных странах.

Изучение натуральных чисел

Тут все максимально просто. Эти числа возникли, как только человеку понадобилось считать – будь то куски мяса или количество бревен для дома.

Более точное изучение натуральных чисел начинается в Древнем Египте и Древней Месопотамии, а это более 6 тысяч лет назад.

А современные математики опираются на то, что после себя оставил древнегреческий ученый Пифагор. Он как раз активно собирал египетские и вавилонские данные, а после отразил их в своих трудах.

Открытие нуля

Конечно, египтяне, вавилоняне и даже греки знали о существовании нуля. Но не считали его числом, а потому не пользовались им. Это, кстати, приносило им немало сложностей. Они порой часами решали задачки, которые нынешний школьник посчитает за минуту.

Открытие отрицательных чисел

Но признание они получили лишь в 17 веке, после того как известный Рене Декарт создал свою систему координат.

В ней он также использовал нуль, привязав к нему положительные и отрицательные числа. Одни находились справа от него, а другие – слева.

Свойства целых чисел

Всем целым числам свойственны следующие характеристики:

Если А и В – целые, то А+В=целое, А-В=целое и А*В=целое

(А + В) + С = А + (В + С)

А + В = В + А, А * В = В * А

А + 0 = 0, А – 0 = 0

А * А = АА, А * (-А) = -АА, (-А) * (-А) = АА

Добавим: точно такое же правило действует и при делении. Минус на минус дают плюс. А минус на плюс или плюс на минус всегда дают минус.

Вместо заключения

Мы уже рассказали, с каким трудом в нашу жизнь попали отрицательные числа. Но сегодня они широко используются не только в математике.

Ну и, наконец, слова положительный и отрицательный используются и в более разговорном смысле, как синонимы хорошего и плохого.

Например, в книгах и фильмах обязательно есть положительные и отрицательные герои. Также и наши черты характера, эмоции и поступки можно разделить на эти две категории.

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Сами по себе числа ничего не значат, будь они даже целыми и натуральными, чтобы в них был смысл, они должны иметь привязку к чему-либо. Например, единица меньше пятидесяти, но всегда ли единица меньше? Если я скажу, что один рубль меньше пятидесяти копеек, то это будет ложью.

В математике , А отрицательное число представляет собой противоположное. В действительной системе счисления отрицательное число - это число меньше нуля . Отрицательные числа часто используются для обозначения величины убытков или дефицита. Причитающийся долг можно рассматривать как отрицательный актив, уменьшение некоторого количества может рассматриваться как отрицательное увеличение. Если величина, такая как заряд электрона, может иметь одно из двух противоположных значений, тогда можно выбрать различие между этими чувствами - возможно, произвольно - как положительное и отрицательное . Отрицательные числа используются для описания значений по шкале ниже нуля, например шкалы Цельсия и Фаренгейта для температуры. Законы арифметики для отрицательных чисел гарантируют, что здравое представление об обратном отражено в арифметике. Например, - (- 3) = 3, потому что исходное значение противоположно противоположному.

Каждое действительное число, кроме нуля, либо положительно, либо отрицательно. Неотрицательные целые числа называются натуральными числами (т. Е. 0, 1, 2, 3 . ), а положительные и отрицательные целые числа (вместе с нулем) называются целыми числами . (Некоторые определения натуральных чисел исключают ноль.)

В бухгалтерском учете суммы задолженности часто обозначаются красными числами или числами в скобках в качестве альтернативного обозначения для представления отрицательных чисел.

СОДЕРЖАНИЕ

Вступление

В результате вычитания

Отрицательные числа можно рассматривать как результат вычитания большего числа из меньшего. Например, отрицательное число три является результатом вычитания трех из нуля:

Как правило, вычитание большего числа из меньшего дает отрицательный результат, причем величина результата представляет собой разницу между двумя числами. Например,

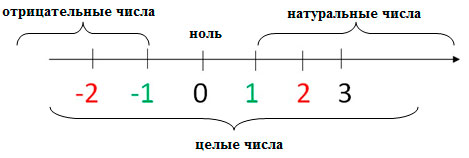
Числовая строка

Связь между отрицательными числами, положительными числами и нулем часто выражается в виде числовой линии :

Цифры, расположенные правее в этой строке, больше, а числа, расположенные левее, меньше. Таким образом, ноль появляется посередине, положительные числа находятся справа, а отрицательные - слева.

Обратите внимание, что отрицательное число с большей величиной считается меньшим. Например, даже если (положительный) 8 больше, чем (положительный) 5 , написано

отрицательный 8 считается меньше отрицательного 5 :

(Потому что, например, если у вас есть -8 фунтов стерлингов, то есть долг в 8 фунтов стерлингов, у вас будет меньше после добавления, скажем, 10 фунтов стерлингов, чем если бы у вас было −5 фунтов стерлингов.) Отсюда следует, что любое отрицательное число меньше, чем любое положительное число, поэтому

Подписанные числа

В контексте отрицательных чисел число больше нуля называется положительным . Таким образом, любое действительное число, кроме нуля, является либо положительным, либо отрицательным, в то время как сам ноль не считается имеющим знак. Положительные числа иногда пишутся со знаком плюс впереди, например +3 обозначает положительную тройку.

Поскольку ноль не является ни положительным, ни отрицательным, термин неотрицательный иногда используется для обозначения положительного или нулевого числа, в то время как неположительный используется для обозначения отрицательного или нулевого числа. Ноль - нейтральное число.

Повседневное использование отрицательных чисел

Спорт

Разница мячей в ассоциациях футбола и хоккея ; разница в очках в регби ; чистая скорость бега в крикете ; результаты игры в гольф относительно номинала .
Плюс-минус дифференциал в хоккее : разница в общем количестве голов, забитых командой (+) и командой (-), когда конкретный игрок находится на льду, является рейтингом игрока +/–. У игроков может быть отрицательный (+/–) рейтинг.
Дифференциал забегов в бейсболе : разница забегов отрицательна, если команда разрешила больше забегов, чем они забили.
С клубов могут вычитаться баллы за нарушение законов, и, таким образом, у клубов может быть отрицательное общее количество баллов до тех пор, пока они не заработают хотя бы такое количество баллов в этом сезоне.
Время круга (или сектора) в Формуле 1 может быть указано как разница по сравнению с предыдущим кругом (или сектором) (например, предыдущим рекордом или кругом, только что пройденным водителем, идущим впереди), и будет положительным, если оно будет медленнее и отрицательный, если быстрее.
В некоторых соревнованиях по легкой атлетике , таких как спринтерские гонки , преодоление препятствий , тройной прыжок и прыжок в длину , помощь от ветра измеряется и записывается и является положительной для попутного ветра и отрицательной для встречного ветра.

Наука

Температура ниже 0 ° C или 0 ° F.
Широта к югу от экватора и долгота к западу от нулевого меридиана .
Топографическим характеристикам земной поверхности задается высота над уровнем моря , которая может быть отрицательной (например, отметка поверхности Мертвого моря или Долины Смерти , или отметка приливного туннеля Темзы ).
Электрические схемы . Когда батарея подключена с обратной полярностью, считается, что приложенное напряжение противоположно ее номинальному напряжению. Например, на 6-вольтовую батарею, подключенную в обратном направлении, подается напряжение -6 вольт.
Ионы имеют положительный или отрицательный электрический заряд.
Импеданс радиовещательной башни AM, используемой в многонаправленных направленных антенных решетках, может быть положительным или отрицательным.

Финансы

Другой

Нумерация этажей в доме ниже первого этажа.
При воспроизведении аудиофайла на портативном медиаплеере , таком как iPod , на экране дисплея может отображаться оставшееся время в виде отрицательного числа, которое увеличивается до нуля с той же скоростью, что и время, которое уже воспроизведено, увеличивается с нуля.
Телевизионные игровые шоу :
- Участники QI часто заканчивают с отрицательными баллами.
- Команды на University Challenge получают отрицательную оценку, если их первые ответы неверны и прерывают вопрос.
- Опасность!имеет отрицательный денежный балл - участники играют на определенную сумму денег, и любой неправильный ответ, который стоит им больше, чем они имеют сейчас, может привести к отрицательному баллу.
- В Цене Is Right " цены игр s купить или продать, если сумма денег теряются , что больше , чем сумма , в настоящее время в банке, он берет на себя отрицательную оценку.
Арифметика с отрицательными числами

Например, выражение 7 + −5 может быть более ясным, если записать 7 + (−5) (даже если формально они означают одно и то же). Вычитание выражение 7 - 5 представляет собой другое выражение , которое не представляет собой одни и те же операции, но он оценивает к тому же результату.

Иногда в начальной школе перед числом может стоять верхний индекс минус или плюс, чтобы явно различать отрицательные и положительные числа, как в

Добавление

Наглядное представление сложения положительных и отрицательных чисел. Большие шары представляют собой числа с большей величиной.

Сложение двух отрицательных чисел очень похоже на сложение двух положительных чисел. Например,

Идея состоит в том, что два долга можно объединить в один долг большей величины.

При сложении смеси положительных и отрицательных чисел можно рассматривать отрицательные числа как вычитаемые положительные величины. Например:

В первом примере кредит 8 сочетается с задолженностью 3 , что дает общий кредит 5 . Если отрицательное число имеет большую величину, результат будет отрицательным:

(−8) + 3 = 3-8 = −5 и 2 + (−7) = 2-7 = −5 .

Здесь кредит меньше долга, поэтому чистый результат - это долг.

Вычитание

Как обсуждалось выше, вычитание двух неотрицательных чисел может дать отрицательный ответ:

Как правило, вычитание положительного числа дает тот же результат, что и добавление отрицательного числа равной величины. Таким образом

С другой стороны, вычитание отрицательного числа дает тот же результат, что и добавление положительного числа равной величины. (Идея состоит в том, что потеря долга - это то же самое, что и получение кредита.) Таким образом,

Умножение

При умножении чисел величина продукта всегда является просто произведением двух величин. Знак продукта определяется следующими правилами:
- Произведение одного положительного числа и одного отрицательного числа отрицательно.
- Произведение двух отрицательных чисел положительно.
Причина первого примера проста: сложение трех −2 вместе дает −6 :

(−2) × 3 = (−2) + (−2) + (−2) = −6 .

Обоснование второго примера более сложное. Идея снова заключается в том, что потеря долга - это то же самое, что получение кредита. В этом случае потерять два долга по три штуки в каждом - это то же самое, что получить кредит в шесть:

(-2 долга ) × (-3 каждый ) = +6 кредита.

Условие, что произведение двух отрицательных чисел является положительным, также необходимо для того, чтобы умножение соответствовало закону распределения . В этом случае мы знаем, что

(−2) × (−3) + 2 × (−3) = (−2 + 2) × (−3) = 0 × (−3) = 0 .

Поскольку 2 × (−3) = −6 , произведение (−2) × (−3) должно равняться 6 .

Эти правила приводят к другому (эквивалентному) правилу - знак любого продукта a × b зависит от знака a следующим образом:
- если a положительно, то знак a × b такой же, как знак b , и
- если a отрицательно, то знак a × b противоположен знаку b .
Обоснование того, почему произведение двух отрицательных чисел является положительным числом, можно найти при анализе комплексных чисел .

Разделение

Знаковые правила для деления такие же, как и для умножения. Например,

8 ÷ (−2) = −4 , (−8) ÷ 2 = −4 ,

Если у делимого и делителя один и тот же знак, результат будет положительным, если у них разные знаки, результат будет отрицательным.

Отрицание

Отрицательная версия положительного числа называется его отрицанием . Например, −3 - это отрицание положительного числа 3 . Сумма ряда и его отрицание равно нулю:

То есть отрицание положительного числа является аддитивным обратным числом.

Используя алгебру , мы можем записать этот принцип как алгебраическое тождество :

х + (- х ) = 0 .

Это тождество верно для любого положительного числа x . Его можно заставить действовать для всех действительных чисел, расширив определение отрицания до нуля и отрицательных чисел. Конкретно:
- Отрицание 0 равно 0, и
- Отрицание отрицательного числа - соответствующее положительное число.
Например, отрицание −3 равно +3 . В основном,

- (- х ) = х .

Абсолютное значение из числа является неотрицательным числом с той же величиной. Например, абсолютное значение −3 и абсолютное значение 3 равны 3 , а абсолютное значение 0 равно 0 .

Формальное построение отрицательных целых чисел

Подобно рациональным числам , мы можем расширить натуральные числа N до целых Z , определив целые числа как упорядоченную пару натуральных чисел ( a , b ). Мы можем расширить сложение и умножение на эти пары по следующим правилам:

( a , b ) + ( c , d ) = ( a + c , b + d ) ( a , b ) × ( c , d ) = ( a × c + b × d , a × d + b × c )

Мы определяем отношение эквивалентности ~ на этих парах по следующему правилу:

( a , b ) ~ ( c , d ) тогда и только тогда, когда a + d = b + c .

Это отношение эквивалентности совместимо с определенными выше сложением и умножением, и мы можем определить Z как фактормножество N ² / ~, т.е. мы идентифицируем две пары ( a , b ) и ( c , d ), если они эквивалентны в выше смысла. Обратите внимание, что Z , снабженный этими операциями сложения и умножения, представляет собой кольцо и фактически является прототипом кольца.

Мы также можем определить общий порядок на Z , написав

( a , b ) ≤ ( c , d ) тогда и только тогда, когда a + d ≤ b + c .

Это приведет к аддитивному нулю вида ( a , a ), аддитивному инверсному к ( a , b ) виду ( b , a ), мультипликативной единице вида ( a + 1, a ) и a определение вычитания

( a , b ) - ( c , d ) = ( a + d , b + c ).

Эта конструкция является частным случаем конструкции Гротендика .

Уникальность

Отрицательное число уникально, как показывает следующее доказательство.

Пусть x - число, а y - его отрицательное значение. Предположим, что y ′ - еще одно отрицательное значение x . По аксиоме действительной системы счисления

Итак, x + y ′ = x + y . Используя закон сокращения для сложения, видно, что y ′ = y . Таким образом, y равно любому другому отрицательному значению x . То есть y - единственный минус x .

История

Отрицательные числа впервые в истории появляются в Девяти главах математического искусства ( Jiu zhang suan-shu ), которые в своем нынешнем виде относятся к периоду династии Хань (202 г. до н.э. - 220 г. н.э.), но могут содержать намного более старый материал. Математик Лю Хуэй (ок. III в.) Установил правила сложения и вычитания отрицательных чисел. Историк Жан-Клод Марцлофф предположил, что важность двойственности в китайской натурфилософии облегчила китайцам принятие идеи отрицательных чисел. Китайцы умели решать одновременные уравнения с отрицательными числами. В Девяти главах использовались красные счетные стержни для обозначения положительных коэффициентов и черные стержни для отрицательных. Эта система является полной противоположностью современной печати положительных и отрицательных чисел в области банковского дела, бухгалтерского учета и торговли, где красные числа обозначают отрицательные значения, а черные числа обозначают положительные значения. Лю Хуэй пишет:

Теперь есть два противоположных вида стержней для подсчета прибылей и убытков, назовем их положительными и отрицательными. Красные счетные стержни - положительные, черные - отрицательные.

К XII веку преемники аль-Караджи должны были сформулировать общие правила знаков и использовать их для решения полиномиальных делений . Как пишет ас-Самаваль :

произведение отрицательного числа - ан-наких - на положительное число - аз-заид - отрицательно, а на отрицательное число положительно. Если мы вычтем отрицательное число из большего отрицательного числа, остаток будет их отрицательной разницей. Разница останется положительной, если мы вычтем отрицательное число из меньшего отрицательного числа. Если мы вычтем отрицательное число из положительного, остаток будет их положительной суммой. Если мы вычтем положительное число из пустой степени ( martaba khāliyya ), остаток будет таким же отрицательным, а если мы вычтем отрицательное число из пустой степени, остаток будет таким же положительным числом.

В средневековой математике Индии преобладали вычислительно-алгоритмические методы и отсутствовали попытки построения дедуктивных систем. Геометрия индийцев – также практическая. И это неудивительно, так как в основном все сюда приносилось из других мест, в том числе и наука – сначала вместе с религиозными эмигрантами из Византии, а потом с деятелями мусульманской экспансии. Соединение здесь различных потоков знания дало свои результаты, и весьма неплохие.

Но и в Индии есть мифический период в развитии математики. Согласно традиции, самыми ранними памятниками математической культуры индийцев являются религиозные книги: сутры и веды. Их происхождение относят к VIII–VII векам до н. э. В них приводились геометрические построения, составляющие важную часть ритуальных условий при постройке культовых сооружений: храмов, алтарей и прочего, а потому в них можно найти первые способы квадрирования кругов и применение теоремы Пифагора. Видимо, как следствие архитектурных требований решалась и арифметическая задача о нахождении пифагоровых троек натуральных чисел.

Числовая система с древних времен определилась как десятичная. Столь же рано сложилась склонность к оперированию большими числами, нашедшая отражение в легендах. Будда, например, отличался феноменальным умением считать; он строил числовые десятичные системы до 10, давая наименования каждому разряду. Женихи прекрасной богини Земли, добиваясь ее руки, обязаны были соревноваться в письме, арифметике, борьбе и стрельбе из лука. Победитель соревнования Сарватасидда придумал, в частности, шкалу чисел, идущих в геометрической прогрессии со знаменателем 100, до числа с 421 нулем. Пристрастие к операциям с большими числами сохранялось в течение всей истории математики в Индии. Но мы не знаем, к какому реально периоду времени эти труды относятся.

Появление позиционного принципа в индийской математике относят к V веку.[23] Отныне числовое значение каждой цифры определялось ее местом влево от конца цифрового ряда. Передвижение цифры на одно место увеличивало ее числовое значение в 10 раз. В соответствии с десятичным принципом индийцы разработали знаки для 9 цифр и десятый знак, нуль. Знак нуля (шунья – пустой) сначала обозначался точкой, потом кружком. И кстати, по некоторым другим сведениям, первые записи с нулем датируются 876 годом.

Арабы (раньше всего в Багдадском халифате) узнали о математических открытиях индийцев в VIII веке благодаря торговым и дипломатическим сношениям. Подхваченная арабами цифровая система пришла в Западную Европу под названием арабской к XII веку, по-видимому, через арабские владения в Испании. Слово сифр, впоследствии принятое в европейских странах для обозначения цифр вообще, исходно значило по-арабски нуль. В английском языке до сих пор слово cipher означает нуль, цифру, шифр.

Наиболее яркий период развития, оставивший самые значительные образцы математической литературы это V–XII века. В это время трудились выдающиеся индийские ученые, математики и астрономы: Ариабхатта (считается, что он жил в конце V века), Брахмагупта (считается, что он родился в 598 году), Магавира (IX век), Бхаскара Акарья (родился в 1114 году) и другие.

Главной особенностью индийской математики является преобладание вычислительных приемов, преподносимых учащимся или читателям в догматической форме.

Представление о бесконечно больших числах ввел в математику Бхаскара. Он пояснял, что бесконечно большое – это тоже число, но не претерпевающее изменений, приращения или ущерба, какое бы большое число мы к нему ни прибавляли или от него ни отнимали; его, по выражению Бхаскары, можно уподобить вечному времени бесконечной цепи существования.

Индийские математики ввели в расчеты и правильно трактовали понятие отрицательного числа. Это пример, как иной подход к проблеме позволяет получать другие результаты. Ведь византийцы работали с отрезками прямых, представить себе отрезок отрицательной длины невозможно. Да и нулевой отрезок имеет мало смысла.

Другое дело – индийская математика. Брахмагупта разъясняет, что числа могут трактоваться либо как имущество, либо как долг. Правила операций с числами тогда таковы: сумма двух имуществ есть имущество, двух долгов – долг, имущества и долга – их разность, которая либо долг, если он больше, либо имущество, если оно больше, либо нуль, если они равны. Сумма нуля и долга есть долг, имущества и нуля – имущество. Произведение двух имуществ или двух неимуществ есть имущество; результат произведения имущества на долг представляет убыток. То же правило справедливо и при делении. Квадрат имущества, или долга, есть имущество; имущество имеет два корня: один составляет прибыль, другой – долг. Корня убытка не существует, ибо таковой не может быть квадратом. Однако, вводя отрицательные числа, индийские математики не использовали их как равноправные элементы математики, считая их только чем-то вроде логических возможностей, потому что, по выражению Бхаскары, люди с ними не согласны.

Развитие методов решения задач неопределенного или диофантова анализа представляет одно из высших достижений индийской математики. Причина заинтересованности математиков Индии в решении подобных задач лежит, по-видимому, в необходимости изучения периодически повторяющихся явлений, обильные примеры чего дает астрономия. В самом деле, вопрос о периоде времени, состоящем одновременно из целого числа дней (х) и целого числа лет (у), приводит к неопределенному уравнению: 10 960 у = 30 х. Другие вопросы, например, о периоде совпадения некоторых явлений, приводят к полным неопределенным уравнениям. Индийские ученые умели находить целочисленные решения различных видов неопределенных уравнений 1-й и 2-й степени.

Но характерная форма изложения, при которой не воспроизводится ни ход рассуждений, ни доказательства, не дает возможности судить о теоретико-числовых методах индийских математиков, хотя то немногое, что известно, показывает на наличие ряда таких методов.

В истории Индии имеется много фактов, свидетельствующих об экономических и политических связях с византийским и арабским миром и с Китаем. В математике считается бесспорным индийское происхождение десятичной системы счисления с нулем и правил счета. Можно проследить заимствование индусами от византийцев некоторых геометрических фактов и т. д.

В заключение еще раз отметим, что как о китайской, так и об индийской математике мы располагаем вообще очень ограниченным запасом сведений.

Читайте также: