Чем больше степень дисперсии собственности

Обновлено: 14.05.2024

Дисперсия - это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая - значения сравнительно близки друг к другу, если большая - далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии - среднеквадратическое отклонение $\sigma(X)=\sqrt$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: "Дисперсия - это второй центральный момент случайной величины" (напомним, что первый начальный момент - это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле: $$ D(X)=M(X-M(X))^2, $$ которую также часто записывают в более удобном для расчетов виде: $$ D(X)=M(X^2)-(M(X))^2. $$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид: $$ D(X)=\sum_^-\left(\sum_^ \right)^2. $$ Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом: $$ D(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx - \left( \int_<-\infty>^ <+\infty>f(x) \cdot x dx \right)^2. $$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения: $$ x_i \quad 1 \quad 2 \\ p_i \quad 0.5 \quad 0.5 $$ и $$ y_i \quad -10 \quad 10 \\ p_i \quad 0.5 \quad 0.5 $$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором - дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии: $$ D(X)=\sum_^-\left(\sum_^ \right)^2 =\\ = 1^2\cdot 0.5 + 2^2 \cdot 0.5 - (1\cdot 0.5 + 2\cdot 0.5)^2=2.5-1.5^2=0.25. $$ $$ D(Y)=\sum_^-\left(\sum_^ \right)^2 =\\ = (-10)^2\cdot 0.5 + 10^2 \cdot 0.5 - (-10\cdot 0.5 + 10\cdot 0.5)^2=100-0^2=100. $$ Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $\sigma(X)=0.5$, $\sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором - на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения: $$ x_i \quad -1 \quad 2 \quad 5 \quad 10 \quad 20 \\ p_i \quad 0.1 \quad 0.2 \quad 0.3 \quad 0.3 \quad 0.1 $$

Снова используем формулу для дисперсии дискретной случайной величины: $$ D(X)=M(X^2)-(M(X))^2. $$ В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание: $$ M(X)=\sum_^ =-1\cdot 0.1 + 2 \cdot 0.2 +5\cdot 0.3 +10\cdot 0.3+20\cdot 0.1=6.8. $$ Потом математическое ожидание квадрата случайной величины: $$ M(X^2)=\sum_^ = (-1)^2\cdot 0.1 + 2^2 \cdot 0.2 +5^2\cdot 0.3 +10^2\cdot 0.3+20^2\cdot 0.1=78.4. $$ А потом подставим все в формулу для дисперсии: $$ D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16. $$ Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x \in(0,6)$ и $f(x)=0$ в остальных точках.

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

Введите число значений случайной величины К.
Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
Нажмите на кнопку "Вычислить".
Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Что еще может пригодиться? Например, для изучения основ теории вероятностей - онлайн учебник по ТВ. Для закрепления материала - еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Степень дисперсии уменьшается с увеличением объема инжектированной пробы. Для большинства проточно-инжекционных систем объем инжектируемой пробы составляет 100 - 200 мкл. Длина и диаметр трубок, используемых для прокачивания растворов, существенно влияют на размывание зон. Обычно используют трубки с внутренним диаметром 0 35 - 0 9 мм, при этом их длина должна быть как можно меньше. [2]

Установлено, что степень дисперсии составляет 100 %, когда образец сланцевой глины состоит из 100 % - ного монтмориллонита натрия. Степень дисперсии 60 % отмечается у чистого монтмориллонита кальция. Степень дисперсии зависит от возраста сланцеватой глины: более древние отложения с высоким содержанием ( %) монтмориллонита диспергируются слабее, чем более молодые отложения с меньшим содержанием монтмориллонита. [3]

Ввиду трго, что степень дисперсии воды в нефти зависит от той пропорции, в которой эта две жидкости смешаны между собой, при малом количестве воды нефть эмульгируется скорее и полнее, чем при большом. Благодаря вводу в эмульсию внутренней фазы, взятой в избытке-можно ее разрушить; исходя из этого соображения, иногда бывает полезно вводить воду в фонтанные и газлифтные скважины, дающие малые количества воды, целиком переходящей в эмульсию. [4]

Если в скелете образца пористой среды присутствует погребенная вода, то она вызовет сокращение степени дисперсии размеров поровых каналов , проводящих углеводородную жидкость. [5]

Анализ ( 4) доказал, что при использовании в такой конструкций упомянутых выше электрооптичеоких кристаллов степень дисперсии для области частот, непосредственно примыкающей к синхронной частоте /, невелика. Поэтому модулятор оказывается эффективным в значительной полосе, ширина которой может достигать 600 - - 700 Мгц. Эффективная полоса частот такого модулятора, как показано IB данной статье, является функцией длины модулятора. [7]

Согласно этой теории величина е системы не зависит ни от концентрации солей в воде, ни от степени дисперсии , ни от частоты поля. [8]

Аналогичные изменения имеют место на температурных зависимостях модуля упругости, причем уменьшение высоты максимума потерь сопровождается уменьшением степени дисперсии модуля упругости . В области а-максимума дисперсия модуля может быть четко обнаружена при рассмотрении температур, перекрывающих области Р - и у-процессов; для увлажненных образцов были обнаружены только изменения модуля упругости. [10]

Алмаз в чистом виде представляет собой кристаллическую аллотропную форму углерода с, если он в чистом виде, очень высоким показателем преломления и степенью дисперсии . Это наиболее твердый из известных минералов. [11]

Кроме этих двух моментов - отсутствие воздуха и отказ от измерений в установившемся режиме - еще одним весьма важным фактором метода ША является возможность регулирования степени дисперсии зоны образца . Этот факт является новым в аналитической химии; именно он позволил проектирование систем ПИА, предназначенных для автоматизации конкретных аналитических операций. [12]

Наиболее важным физическим явлением при получении зон пробы и реагента в несегментированном потоке жидкости является их размывание в потоке носителя. Степень дисперсии вдоль зоны неодинакова. В двух крайних частях зоны на границах раздела с носителем она является результатом молекулярной диффузии и конвекции, а в центральной части - только конвекции. При этом дисперсия может проходить как в радиальном, так и в аксиальном направлениях. [14]

С другой стороны, дифракционные решетки обладают линейной зависимостью дисперсии от угла отражения в большом диапазоне исследуемых длин волн, а ширина полосы отражаемого излучения практически не зависит от длины волны. Степень дисперсии определяется числом линий, приходящихся на единицу длины. [15]

…из соображений гуманности сразу весь список :) Тема не самая простая, а точнее, кропотливая, но я научу вас БЫСТРО находить все перечисленные дисперсии, а также расскажу, что они означают и для чего нужны. Для освоения данного урока нужно понимать, что такое дисперсия и группировка данных (предыдущая статья) и уметь выполнять несложные расчёты. Впрочем, всё кратко повторим по ходу пьесы, и я немедленно начинаю разбирать материал:

По данным Примера 55 рассчитать общую, групповые, внутригрупповую и межгрупповую дисперсию

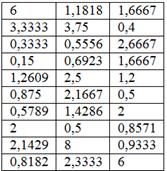
Напоминаю, что в той задаче нам были даны относительные показатели металлоёмкости станков (т/кВт):

и по исходным данным мы сразу вычислили общую среднюю:
т/кВт

Общая дисперсия – показатель не новый, и её мы уже неоднократно рассчитывали ранее. Для этого нужно найти квадраты отклонений вариант от общей средней:

вычислить их сумму и разделить её на объём совокупности:

Вычисления удобно проводить в Экселе, и чуть позже будет ролик по этой теме, буквально минут за 5 разгромим всю задачу.

Общая дисперсия характеризует меру рассеяния значений относительно общей средней . Чем дисперсия больше, тем дальше разбросаны от средней, и наоборот, чем дисперсия меньше, тем они к средней ближе.

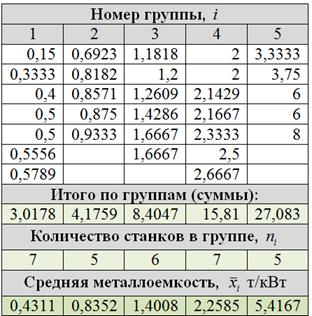
Теперь вычислим групповые дисперсии. Для этого, очевидно, нужно разбить совокупность на группы, при этом группировку можно выполнить разными способами. В Примере 55 мы упорядочили варианты по возрастанию и провели удачную равнонаполненную группировку:

В результате получилось 5 групп объёмом , по которым мы рассчитали групповые средние:

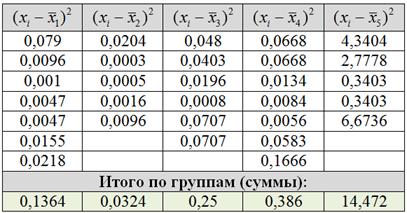
И как вы правильно догадались, у нас будет 5 групповых дисперсий. По каждой группе своя. Для этого нужно рассчитать квадраты отклонений от СВОИХ групповых средних:

Тушеваться не надо, в Экселе мы эти вычисления выполним в несколько щелчков, и если вам не терпится посмотреть, как это происходит, то можно сразу перейти к видеоролику (см. ниже).

Таким образом, групповые дисперсии:

Групповая дисперсия характеризует меру разброса значений группы относительно групповой средней. В нашем примере наименьшей получилась дисперсия по 2-й группе: , это означает, что варианты этой группы расположены достаточно близко к . Максимальная дисперсия – в 5-й группе: , это означает, что многие варианты этой группы расположены достаточно далеко от .

внутригрупповая дисперсия – это средняя, а точнее средневзвешенная арифметическая групповых дисперсий:

И внимательный читатель заметил, что для нахождения внутригрупповой дисперсии не обязательно рассчитывать групповые дисперсии, ибо:
,
т.е. достаточно просуммировать числа нижней строки вышеприведённой таблицы.

И, наконец, ещё одна дисперсия :)

Рассмотрим общую среднюю и групповые средние .

Межгрупповая дисперсия – это дисперсия групповых средних относительно общей средней:

Для компактности удобно оформить небольшую расчётную табличку:

Таким образом:

Межгрупповая дисперсия характеризует меру разброса групповых средних относительно общей средней. Чем эта дисперсия больше, тем дальше расположены групповые средние (многие из них) относительно общей средней .

Для общей, внутригрупповой и межгрупповой дисперсий справедливо так называемое правило сложение дисперсий:

, то есть общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсии.

Примечание: в различных источниках встречаются разные обозначения этих дисперсий, и, кроме того, слагаемые правой части могут быть переставлены.

Проверим, всё ли мы правильно подсчитали:

– получено верное равенство с точностью до погрешности округлений, таким образом, все дисперсии найдены верно.

Как вычислить дисперсии? (Ютуб)

И после изучения технической стороны вопроса вникнем в СМЫСЛ этих дисперсий.

Теперь смотрим на правило сложения дисперсий:
, то есть, общая дисперсия включает в себя внутригрупповую и межгрупповую дисперсию.

Межгрупповая дисперсия характеризует вариацию, обусловленную фактором, который лёг в основу группировки.

Внутригрупповая дисперсия отражает вариацию, обусловленную другими факторами.

Этот коэффициент характеризует долю вариации, объяснённую группировочным фактором.

Эмпирический коэффициент детерминации изменяется в пределах , и чем он ближе к единице, тем сильнее влияние группировочного фактора на вариацию статистической совокупности. Если , то речь идёт о строгой функциональной зависимости, в этом случае , то есть внутригрупповая дисперсия (по правилу сложения) равна нулю: , и это в свою очередь означает, что в каждой группе находятся одинаковые и строго определённые значения (т.е. вариация по группам отсутствует).

Наоборот, чем ближе к нулю, тем влияние группировочного фактора меньше; математически это означает, что межгрупповая дисперсия слишком малА, а это в свою очередь значит, что групповые средние расположены очень близко к общей средней . И логика здесь простА: если мы провели группировку и получили примерно одинаковые средние по группам, то влияние фактора явно слабО. Но это ещё не значит, что сам фактор не важный ;)

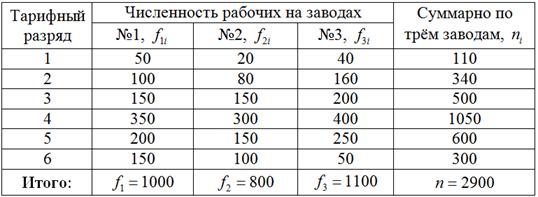
Распределение рабочих трех заводов одного объединения по тарифным разрядам характеризуется следующими данными:

Определить:
а) общую дисперсию;
б) дисперсию по каждому заводу (групповые дисперсии);
в) среднюю из групповых дисперсий (внутригрупповую дисперсию);
г) межгрупповую дисперсию;
д) проверить правило сложения дисперсий
е) вычислить эмпирический коэффициент детерминации и сделать вывод о том, насколько значимо различается квалификация рабочих на заводах. Иными словами, нужно выяснить, нанимали ли на какие-то заводы более квалицированных рабочих, чем на другие, или же квалификация по заводам примерно одинакова?

Следует отметить, что разобранные дисперсии используются и в других задачах математической статистики, где их нужно рассчитывать немного с другой спецификой. И эти задачи уже на подходе ;) На следующем уроке мы познакомимся с аналитической группировкой и гармонично разовьём тему с дисперсиями. Надеюсь, они вам понравились :)

Решения и ответы:

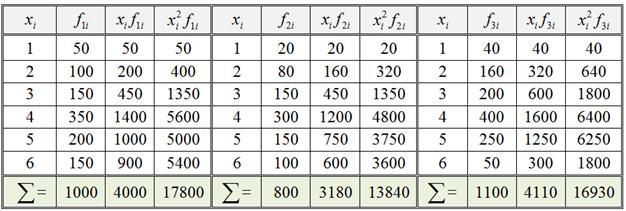
б) Заполним расчётную таблицу для каждой группы:

Найдем средние значения тарифного разряда по заводам (групповые средние):

Вычислим групповые дисперсии:
;

в) Вычислим среднюю из групповых (внутригрупповую) дисперсию:

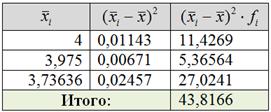
г) Для нахождения межгрупповой дисперсии удобно заполнить расчётную табличку:

или расписать так:

е) Вычислим эмпирический коэффициент детерминации:
, примерно ноль.

Таким образом, средняя квалификация рабочих по заводам практически одинакова (иными словами, фактор, положенный в основу группировки (распределение рабочих по заводам) не оказывает никакого влияния – нельзя сказать, что на какой-то завод специально нанимали более квалифицированных рабочих).

! Примечание: но группировочный фактор сам по себе важен, поскольку распределяет рабочих по заводам. Только вот на тарифные разряды это практически не влияет.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Генеральная совокупность - множество всех объектов, относительно которых предполагается делать выводы при изучении конкретной задачи.

Выборка - часть генеральной совокупности, которая охватывается экспериментом.

Репрезентативная выборка - выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности.

Унимодальное распределение - распределение, имеющее только одну моду (пример: нормальное распределение)

Способы формирования репрезентативной выборки:

Простая случайная выборка (simple random sample)

Стратифицированная выборка (stratified sample)

Групповая выборка (cluster sample)

Типы переменных:

непрерывные (рост в мм)

дискретные (количество публикаций у учёного)

Ранговые (успеваемость студентов)

Гистограмма частот:

Позволяет сделать первое впечатление о форме распределения некоторого количественного признака.

Описательные статистики:

Меры центральной тенденции (узкий диапазон, высокие значения признака):

Мода (mode) - значение во множестве наблюдений, которое встречается наиболее часто.

Медиана (median) - значение признака, которое делит упорядоченное множество пополам.

Среднее значение (mean, среднее арифметическое) - сумма всех значений измеренного признака, делённая на количество измеренных значений.

( используется для среднего значения из выборки, а для генеральной совокупности латинская буква )

Свойства среднего:

Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.

Если для каждого значения выборки, рассчитать такой показатель как его отклонение от среднего арифметического, то сумма этих отклонений будет равняться нулю.

Меры изменчивости (широкий диапазон, вариативность признака):

Размах (range) - разность максимального и минимального значения.

При добавлении сильно отличающегося значения данные меняются сильно и могут быть некорректные.

Дисперсия (variance) - средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия генеральной совокупности:

(среднеквадратическое отклонение генеральной совокупности)

(среднеквадратическое отклонение выборки)

Свойства дисперсии:

Квартили распределения и график box-plot

Квартили - три точки (значения признака), которые делят упорядоченное множество данных на четыре равные части.

Box-plot - такой вид диаграммы в удобной форме показывает медиану (или, если нужно, среднее), нижний и верхний квартили, минимальное и максимальное значение выборки и выбросы.

Нормальное распределение

Отклонения наблюдений от среднего подчиняются определённому вероятностному закону.

Стандартизация

Стандартизация или z-преобразование - преобразование полученных данных в стандартную Z-шкалу (Z-scores) со средним и

Правило "двух" и "трёх" сигм

Центральная предельная теорема

Центральная предельная теорема - класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения.

Есть признак, распределенный КАК УГОДНО* с некоторым средним и некоторым стандартным отклонением. Тогда, если выбирать из этой совокупности выборки объема n, то их средние тоже будут распределены нормально со средним равным среднему признака в ГС и стандартным отклонением .

Стандартная ошибка среднего - теоретическое стандартное отклонение всех средних выборки размера , извлекаемое из совокупности.

Доверительные интервалы для среднего

Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента).

Идея статистического вывода

P-значение (P-value) - величина, используемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода).

2. Сравнение средних

T-распределение

Если число наблюдений невелико и \sigma неизвестно (почти всегда), используется распределение Стьюдента (t-distribution).

Унимодально и симметрично, но: наблюдения с большей вероятностью попадают за пределы от

"Форма" распределения определяется числом степеней свободы ().

С увеличением числа распределение стремится к нормальному.

t-распределение используется не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности.

Сравнение двух средних; t-критерий Стьюдента

Критерий, который позволяет сравнивать средние значения двух выборок между собой, называется t-критерий Стьюдента.

Условия для корректности использования t-критерия Стьюдента:

Две независимые группы

Формула стандартной ошибки среднего:

Формула числа степеней свободы:

Формула t-критерия Стьюдента:

Переход к p-критерию:

Проверка распределения на нормальность, QQ-Plot

Однофакторный дисперсионный анализ

Часто в исследованиях необходимо сравнить несколько групп между собой. В таком случае применятся однофакторный дисперсионный анализ.

Незвисимая переменная - номинативная перменная с нескольким градациями, разделяющая наблюдения на группы.

Зависимая перемнная - количественная переменная, по степени выраженности которой сравниваются группы.

Читайте также: