Обеспечить вычисление интеграла с заданной точностью можно используя

Обновлено: 02.07.2024

Методическое пособие предназначено как для студентов специальности 220400 “Программное обеспечение вычислительной техники и автоматизированных систем” для изучения дисциплины “Программирование на языке высокого уровня”, так и для других технических специальностей по информатике или основам программирования.

Составители: Белозеров Е.С., доц.

Рецензент Иванов В.И., доц., канд. техн. наук

ЦЕЛЬ РАБОТЫ

1. Закрепление навыков алгоритмизации и программирования с применением подпрограмм-функций.

2. Освоение навыков создания новых типов данных с помощью оператора typedef.

3. Передача сложных типов данных через механизм формальных/фактических параметров.

4. Знакомство с простейшими методами численного интегрирования функций.

Алгоритмы численного интегрирования функций

Определенный интеграл от функции f(x) легко вычисляется по формуле Ньютона-Лейбница

если мы располагаем аналитической формулой её первообразной F(x).

Однако при решении практических и экспериментальных задач очень редко удаётся выразить F(x) через элементарные функции и поэтому приходится искать интеграл I приближенными численными методами с помощью квадратурных формул, то есть путем вычисления площадей.

Простейшими методами численного интегрирования являются метод прямоугольников, трапеций и парабол (Симпсона). Рассмотрим их алгоритмы.

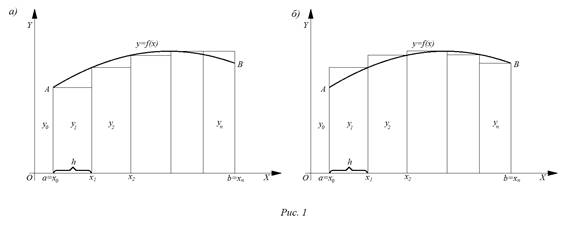
В методе прямоугольников значение интеграла (т.е. площади криволинейной трапеции) на интервале (a, b) заменяется суммой площадей прямоугольников в соответствии с рисунком

где h - шаг интегрирования, расстояние между узлами x₀, x₁, x₂, x₃, .

Каждый прямоугольник имеет высоту f(x_i) и ширину h =(b-a)/n и поэтому расчетная формула очень проста

Кстати, она вытекает из определения понятия интеграла, как предела интегральной суммы при устремлении числа отрезков n к бесконечности.

Приведенные на рисунке 1 варианты построения прямоугольников (левые, правые и центральные) различаются точностью вычисления I_п (при одинаковом n).

Разработаем универсальный алгоритм вычисления приближенного вычисления интеграла I_п.

Из формулы (2) очевидно, что надо в цикле меняя x от a до b с шагом h надо вычислять f(x) и накапливать сумму S по известному рекуррентному алгоритму

S = S +f(x),

Заодно можно накапливать и текущее значение аргумента x = x +h.

Для этого вначале ячейку S надо обнулить, S=0, и установить начальное значение x по универсальной формуле (годящейся трех вариантов)

x = a + c * h (3)

где c- смещение первого узла x₀ относительно нижнего предела a,

при c = 0 будут левые прямоугольники, c = 1 - правые, а при c = 0.5 центральные.

Таким образом, схема алгоритма вычисления интеграла (2) будет иметь вид.

Как хорошо видно на рисунке 1 центральные прямоугольники более плотно прилегают к нашей функции f(x), а погрешности левой и правой частей каждого прямоугольника взаимно компенсируются. Поэтому центральные прямоугольники работают значительно точнее.

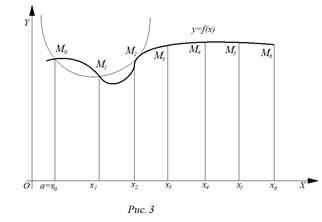
В методе парабол используют полученную Симпсоном квадратурную формулу, согласно которой криволинейная трапеция на участке из трех узлов x₀, x₁, x₂. заменяется площадью параболы (см. рисунок 3).

Нечетные ординаты имеют коэффициент 4 согласно формуле Симпсона, а у четных - коэффициент 2, поскольку они учитываются дважды у левой параболы и у правой. Неудобство формулы (5) в том, что число четных (внутренних) ординат, с учетом коэффициента 2 на 2 штуки меньше чем нечетных. Для упрощения алгоритма надо выровнять суммы для реализации расчетов в одном цикле. Тогда вторая сумма учтет две лишних ординаты f_n = f_b , поэтому их надо отнять. В результате получим

Принимая как в предыдущем методе шаг интегрирования h =(b-a)/n, организуем цикл по параболам, изменяя номер i от 1 до m = n/2 и аргумент x с шагом 2 h.

При этом, вместо обнуления ячейки S, запишем вначале туда разность крайних ординат

а в качестве начального значения аргумента x примем узел x₁ ,т.е.

x = a +h

Сумму S согласно (5') накапливаем по формуле

S = S + 4f(x) +2 f(x+h).

Таким образом, получаем схему алгоритма вычисления интеграла методом Симпсона (рисунок 5).

В результате из формул (2) и (5) мы получили компактные и удобные алгоритмы численного интегрирования при заданном числе шагов n. Проблема в том, что мы не знаем заранее, как выбрать приемлемое число шагов интегрированияn . При одних n точность будет хорошая при другом не очень, всё зависит от свойств интегрируемой функции.

С другой стороны мы всегда можем назначить подходящее значение точности (или погрешности расчетов). Для этого надо уметь оценивать точность расчетов и разработать алгоритм, который бы сам останавливался по достижению заданной точности.

3 Оценка погрешностей методов

Абсолютной погрешностью называют разность между истинным x_и и приближённым x_П значением измеряемой (вычисляемой) величины

e_а = | x_и - x_п|, (6)

модуль берут исключительно для удобства.

К сожалению, абсолютная погрешность зависит от самой измеряемой величины, поэтому на практике используют относительную (относительно самой измеряемой величины) погрешность

которая не зависит от самой измеряемой величины x.

Для наших расчетов, в принципе можно пользоваться любой погрешностью e_а или e_от..

Для рассмотренных методов численного интегрирования известны теоретические формулы для оценки погрешности каждого метода, которые сведены в таблице 1.

Таблица 1. Погрешности методов численного интегрирования (8)

1	метод левых и правых прямоугольников
2	метод центральных прямоугольников
3	метод трапеций
4	метод парабол (Симпсона)

где ξ- такой x, при котором производные максимальны.

К сожалению, пользоваться формулами теоретической погрешности для остановки алгоритмов мы не можем, т.к. они зависят производных и надо решать экстремальную задачу, что значительно сложнее, чем само интегрирование. Формулы из табл. 1 позволяют нам только сравнивать и оценивать алгоритмы, что само по себе весьма существенно.

Например, формула 1 для правых прямоугольников, говорит нам, что погрешность (точность) метода пропорциональна шагу интегрирования h и значению первой производной f(x).

Метод центральных прямоугольников обеспечивает точность пропорциональную квадрату шага h и значению второй производной f"(x), а метод Симпсона - четвертой степени h и значению четвертой производной - f IV (x).

Это означает, что метод левых прямоугольников дает нулевую погрешность для линейной функции f(x) = a+ bx, метод центральных прямоугольников для квадратичной функции f(x) = a+ bx + c x 2 , а метод Симпсона даст нулевую погрешность для кубической параболы.

Кроме того, трактовка формул (8) позволяют нам судить об эффективности разных методов. Формулы (8) говорят нам, что при уменьшении шага в два раза погрешность расчетов по методу левых прямоугольников должна уменьшиться в два раза (что не очень здорово), по методу центральных прямоугольников - в четыре раза, а по методу Симпсона - аж - в 2 4 =16 раз. В этом студент сможет убедиться в своих программах.

Проблема получения алгоритма численного интегрирования по заданной точности (погрешности) остаётся.

Для этого можно воспользоваться традиционным методом проб и ошибок или принципом двойного просчета.

Численное интегрирование по заданной точности

Для вычисления интеграла (1) по заданной точности e_зад нам нужна формула для вычисления текущей (достигнутой) погрешности. При этом, имеющиеся формулы (8), как отмечалось, нам не годятся. Для этого используют следующую целесообразную идею, называемую "принцип двойного просчета", которая заключается в следующем.

Очевидно, что точность растет с увеличением числа шагов n.

Возьмём вначале достаточно малое число n = 4. Вычислим при этом n значение интеграла и обозначим его как S0. Удвоим число n = 2*n и снова вычислим значение интеграла S, если разница между S и S0 достаточна мала, значит мы достигли требуемой точности, в противном случае повторим снова удвоим nи вычислим новое S. Как только разница между S и S0 станет меньше e_зад, значит мы достигли требуемой точности и алгоритм надо остановить, в противном случае эти операции надо повторять. Таким образом, для оценки текущей погрешности (и остановки алгоритма) мы выбрали величину

e_тек = | S - S0 |, (9)

где S0 и S - старое и новое (при удвоенном n) значение интеграла.

Для оценки качества нашей программы будем использовать фактическую погрешность (критерий истины), которую мы будем вычислять по формуле (6) как разницу между истинным значением интеграла I_т по формуле Ньютона-Лейбница (с учетом данной нам для контрольного примера - первообразной F(x)) и приближенным значением S.

e_факт = | I_т - S |, (10)

Заметим, что величину e_факт мы не можем использовать для остановки алгоритма, потому, что на практике величина I_т нам известна не будет. Сведем все наши переменные в таблицу.

Переменная	примечание
в алг.	в прог.
Значение интеграла по Ньютону-Лейбницу	I_т	контрольный пример
Число отрезков	n	n
Заданная погрешность	e_зад	ez
Текущая погрешность	e_тек	et
Фактическая погрешность	e_факт	ef
Старое значение интеграла	S0	S0
Новое значение интеграла	S	S

Очевидно также, что в процессе удвоения n ирасчетов интеграла, надо сохранить текущее приближенное значение интеграла S в "старой" ячейке S0. Таким образом, алгоритм численного интегрирования функции по заданной погрешности e_зад, будет иметь вид (рис. 5).

В нашем алгоритме мы предусмотрели расчет и протокол печати, как текущей, так и фактической погрешности. Последняя нужна нам для контроля качества нашей программы. После отладки программы печать протокола можно будет отключить.

Задача численного интегрирования функций заключается в вычислении приближенного значения определенного интеграла:

, (1)

на основе ряда значений подынтегральной функции .< f(x) |x=x_k = f(x_k ) = y_k >.

Формулы численного вычисления однократного интеграла называются квадратурными формулами, двойного и более кратного – кубатурными.

Обычный прием построения квадратурных формул состоит в замене подынтегральной функции f(x) на отрезке [a,b] интерполирующей или аппроксимирующей функцией g(x) сравнительно простого вида, например, полиномом, с последующим аналитическим интегрированием. Это приводит к представлению

В пренебрежении остаточным членом R[f] получаем приближенную формулу

Обозначим через y_i = f(x_i ) значение подинтегральной функции в различных точках на [a,b]. Квадратурные формулы являются формулами замкнутого типа, если x₀ =a , x_n =b.

В качестве приближенной функции g(x) рассмотрим интерполяционный полином на в форме полинома Лагранжа:

, при этом , где - остаточный член интерполяционной формулы Лагранжа.

, (2)

. (3)

В формуле (2) величины <> называются узлами, <> – весами, - погрешностью квадратурной формулы. Если веса <> квадратурной формулы вычислены по формуле (3), то соответствующую квадратурную формулу называют квадратурной формулой интерполяционного типа.

1. Веса <> квадратурной формулы (2) при заданном расположении узлов не зависят от вида подынтегральной функции.

2. В квадратурных формулах интерполяционного типа остаточный член R_n [f] может быть представлен в виде значения конкретного дифференциального оператора на функции f(x). Для

3. Для полиномов до порядка n включительно квадратурная формула (2) точна, т.е. . Наивысшая степень полинома, для которого квадратурная формула точна, называется степенью квадратурной формулы.

Рассмотрим частные случаи формул (2) и (3): метод прямоугольников, трапеций, парабол (метод Симпсона). Названия этих методов обусловлены геометрической интерпретацией соответствующих формул.

Метод прямоугольников

Определенный интеграл функции от функции f(x): численно равен площади криволинейной трапеции, ограниченной кривыми у=0, x=a, x=b, y=f(x) (рисунок. 1).

Рис. 1 Площадь под кривой y=f(x) Для вычисления этой площади весь интервал интегрирования [a,b] разбивается на n равных подинтервалов длины h=(b-a)/n. Площадь под подынтегральной кривой приближенно заменяется на сумму площадей прямоугольников, как это показано на рисунке (2).

Рис. 2 Площадь под кривой y=f(x) аппроксимируется суммой площадей прямоугольников
Сумма площадей всех прямоугольников вычисляется по формуле

(4)

Метод, представленный формулой (4), называется методом левых прямоугольников, а метод, представленный формулой(5) – методом правых прямоугольников:

(5)

Погрешность вычисления интеграла определяется величиной шага интегрирования h. Чем меньше шаг интегрирования, тем точнее интегральная сумма S аппроксимирует значение интеграла I. Исходя из этого строится алгоритм для вычисления интеграла с заданной точностью. Считается, что интегральная сумма S представляет значение интеграла I c точностью eps, если разница по абсолютной величине между интегральными суммами и , вычисленными с шагом h и h/2 соответственно, не превышает eps.

Для нахождения определенного интеграла методом средних прямоугольников площадь, ограниченная прямыми a и b, разбивается на n прямоугольников с одинаковыми основаниями h, высотами прямоугольников будут точки пересечения функции f(x) с серединами прямоугольников (h/2). Интеграл будет численно равен сумме площадей n прямоугольников (рисунок 3).

Рис. 3 Площадь под кривой y=f(x) аппроксимируется суммой площадей прямоугольников

n – количество разбиений отрезка [a,b].

Метод трапеций

Для нахождения определенного интеграла методом трапеций площадь криволинейной трапеции также разбивается на n прямоугольных трапеций с высотами h и основаниями у₁ , у₂ , у₃ . у_n , где n - номер прямоугольной трапеции. Интеграл будет численно равен сумме площадей прямоугольных трапеций (рисунок 4).

Рис. 4 Площадь под кривой y=f(x) аппроксимируется суммой площадей прямоугольных трапеций.

n – количество разбиений

(6)

Погрешность формулы трапеций оценивается числом

Погрешность формулы трапеций с ростом уменьшается быстрее, чем погрешность формулы прямоугольников. Следовательно, формула трапеций позволяет получить большую точность, чем метод прямоугольников.

Формула Симпсона

Если для каждой пары отрезков построить многочлен второй степени, затем проинтегрировать его на отрезке и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона.

В методе Симпсона для вычисления определенного интеграла весь интервал интегрирования [a,b] разбивается на подинтервалы равной длины h=(b-a)/n. Число отрезков разбиения является четным числом. Затем на каждой паре соседних подинтервалов подинтегральная функция f(x) заменяется многочленом Лагранжа второй степени (рисунок 5).

Рис. 5 Функция y=f(x) на отрезке заменяется многочленом 2-го порядка

Рассмотрим подынтегральную функцию на отрезке . Заменим эту подынтегральную функцию интерполяционным многочленом Лагранжа второй степени, совпадающим с y= в точках :

Проинтегрируем на отрезке .:

Введем замену переменных:

Учитывая формулы замены,

Выполнив интегрирование, получим формулу Симпсона:

Полученное для интеграла значение совпадает с площадью криволинейной трапеции, ограниченной осью , прямыми , и параболой, проходящей через точки На отрезке формула Симпсона будет иметь вид:

В формуле параболы значение функции f(x) в нечетных точках разбиения х₁ , х₃ , . х₂ _n _-1 имеет коэффициент 4, в четных точках х₂ , х₄ , . х₂ _n _-2 - коэффициент 2 и в двух граничных точках х₀ =а, х_n =b - коэффициент 1.

Геометрический смысл формулы Симпсона: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами.

Если функция f(x) имеет на [a, b] непрерывную производную четвертого порядка, то абсолютная величина погрешности формулы Симпсона не больше чем

где М - наибольшее значение на отрезке [a, b]. Так как n 4 растет быстрее, чем n 2 , то погрешность формулы Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы трапеций.

Вычислим интеграл

Этот интеграл легко вычисляется:

Возьмем n равным 10, h=0.1, рассчитаем значения подынтегральной функции в точках разбиения , а также полуцелых точках .

По формуле средних прямоугольников получим I_прям =0.785606 (погрешность равна 0.027%), по формуле трапеций I_трап =0.784981 (погрешность около 0,054. При использовании метода правых и левых прямоугольников погрешность составляет более 3%.

Для сравнения точности приближенных формул вычислим еще раз интеграл

но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х₀ =0, х₁ =1/4, х₂ =1/2, х₃ =3/4, х₄ =1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках: у₀ =1,0000, у₁ =0,8000, у₂ =0,6667, у₃ =0,5714, у₄ =0,5000.

По формуле Симпсона получаем

Оценим погрешность полученного результата. Для подынтегральной функции f(x)=1/(1+x) имеем: f (4) (x)=24/(1+x) 5 , откуда следует, что на отрезке [0, 1] . Следовательно, можно взять М=24, и погрешность результата не превосходит величины 24/(2880× 4 4 )=0.0004. Сравнивая приближенное значение с точным, заключаем, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций.

Сравнение методов по точности

Сравним методы по точности, для этого произведем вычисления интеграла функций y=x, y=x+2, y=x 2 , при n=10 и n=60, a=0, b=10. Точное значение интегралов составляет соответственно: 50, 70, 333.(3)

Сертификат и скидка на обучение каждому участнику

Опорный конспект на тему:

Постановка задачи.

2. Формулы прямоугольников.

3. Формула трапеций.

4. Формула Симпсона.

5.Вопросы для самопроверки.

1. Постановка задачи

Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой.

Мы будем рассматривать способы приближенного вычисления определенных интегралов

, основанные на замене интеграла конечной суммой:

где С _k - числовые коэффициенты, а x _k _ [ a, b ], k = 0, 1, …, n .

называется квадратурной формулой, а x _k – узлами квадратурной формулы. Погрешность квадратурной формулы определяется соотношением

В общем случае погрешность квадратурной формулы зависит как от выбора коэффициентов С _к , так и от расположения узлов х _к . Введем на отрезке [ a, b ] равномерную сетку с шагом h , тогда x _i = a + ih , где ( i = 0, 1, . n ;
h·n = b-a ). Теперь выражение (2.1) можно представить в виде суммы интегралов по частичным отрезкам:

Таким образом, для построения формулы численного интегрирования на отрезке [ a, b ] достаточно построить квадратурную формулу на частичном отрезке [ x _i-1 , x _i ] и воспользоваться полученной формулой.

2. Формула прямоугольников

На частичном отрезке [ x _i-1 , x _i ] заменим подынтегральную функцию полиномом Лагранжа нулевого порядка, построенным в одной точке. Естественно в качестве этой точки выбрать среднюю: x _i-0.5 = x _i - 0.5 h . Тогда получим формулу

Получим составную формулу средних прямоугольников:

. Графическая иллюстрация метода средних прямоугольников представлена на рис.

Рис. 1. Интегрирование методом средних прямоугольников

Погрешность формулы прямоугольников определяется выражением

Здесь . Таким образом, погрешность полученной формулы пропорциональна O(h 2 ) .

Замечание. Формулу прямоугольников можно представить в ином виде:

Эти формулы в полученном выражении называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис. 2.

Рис. 2. Метод левых (а) и правых (б) прямоугольников

Однако из-за нарушения симметрии в полученных формулах их погрешность значительно больше, чем в методе средних прямоугольников и ~ O(h).

3. Формула трапеций

Если на частичном отрезке подынтегральную функцию заменить полиномом Лагранжа первой степени, то есть

тогда искомый интеграл запишется следующим образом:

После подстановки данных выражений составная формула трапеций примет вид:

Графически метод трапеций представлен на рис. 3.

Рис. 3. Метод трапеций

Погрешность последней формулы определяется выражением:

Таким образом, погрешность метода трапеций Ψ ~ O(h² ) , но она в два раза больше, чем для формулы средних прямоугольников.

4. Формула Симпсона

В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки
( x _j , f ( x _j )), где j = i -1; i -0.5; i , то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:

Проведя интегрирование, получим:

Это и есть формула Симпсона или формула парабол. На отрезке
[ a, b ] формула Симпсона примет вид

Графическое представление метода Симпсона показано на рис. 4.

Рис. 4. Метод Симпсона

Избавимся в последнем выражении от дробных индексов, переобозначив переменные:

Тогда формула Симпсона примет вид

Погрешность полученной формулы оценивается следующим выражением:

где h·n = b - a , . Таким образом, погрешность формулы Симпсона пропорциональна O ( h 4 ).

Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на четное число интервалов.

2.5. Вычисление определенных интегралов методами Монте–Карло

Рассматриваемые ранее методы называются детерминированными , то есть лишенными элемента случайности.

Методы Монте–Карло (ММК) – это численные методы решения математических задач с помощью моделирования случайных величин. ММК позволяют успешно решать математические задачи, обусловленные вероятностными процессами. Более того, при решении задач, не связанных с какими-либо вероятностями, можно искусственно придумать вероятностную модель (и даже не одну), позволяющую решать эти задачи. Рассмотрим вычисление определенного интеграла

При вычислении этого интеграла по формуле прямоугольников интервал [ a, b ] разбиваем на N одинаковых интервалов, в серединах которых вычислялись значения подынтегральной функции. Вычисляя значения функции в случайных узлах, можно получить более точный результат:

Здесь γ _i - случайное число, равномерно распределенное на интервале
[0, 1]. Погрешность вычисления интеграла ММК ~ , что значительно больше, чем у ранее изученных детерминированных методов.

На рис. 5 представлена графическая реализация метода Монте-Карло вычисления однократного интеграла со случайными узлами:

Рис. 5. Интегрирование методом Монте-Карло (1-й случай)

Однако при вычислении кратных интегралов детерминированными методами оценка погрешности перерастает в задачу порой более сложную, чем вычисление интеграла. В то же время погрешность вычисления кратных интегралов ММК слабо зависит от кратности и легко вычисляется в каждом конкретном случае практически без дополнительных затрат.

Рассмотрим еще один метод Монте-Карло на примере вычисления однократного интеграла:

Рис. 6. Интегрирование методом Монте-Карло (2-й случай)

Как видно на рис. 6, интегральная кривая лежит в единичном квадрате, и если мы сумеем получать пары случайных чисел, равномерно распределенных на интервале [0, 1], то полученные значения (γ _1, γ ₂ ) можно интерпретировать как координаты точки в единичном квадрате. Тогда, если этих пар чисел получено достаточно много, можно приблизительно считать, что
. Здесь S – число пар точек, попавших под кривую, а N – общее число пар чисел.

Пример 1. Вычислить следующий интеграл:

Поставленная задача была решена различными методами. Полученные результаты сведены в табл. 1.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО Разработал преподаватель: Игнатьева Елена Сергеевна Тема: Вычисление интегралов методами численного интегрирования.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема :

Вычисление интегралов методами численного интегрирования.

Цель работы:

- применить теоретический материал по данной теме через решение упражнений;

- применить умения приближенно вычислять интегралы при помощи формул Ньютона-Котеса (формула прямоугольников, формула трапеций, формула парабол (Симпсона)).

Оборудование:

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

Вариант 1 Вариант 2

1. Вычислите интеграл от заданной функции на отрезке при делении отрезка на 10 равных частей тремя способами по формулам: прямоугольников, трапеций, Симпсона.

2.Вычислите интеграл от заданной функции на заданном отрезке способом Гаусса.

Порядок выполнения:

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

Формулы прямоугольников

Формулы прямоугольников имеют вид

(1)

(2)

(3)

Формула (1) называется формулой левых прямоугольников (рис. 1 а), а формула (2) – формулой правых прямоугольников (рис. 1 б).

Абсолютная погрешность метода прямоугольников определяется неравенством

(4)

где .

Формула трапеций.

Формула трапеций имеет вид

(5)

где

Правая часть этой формулы выражает площадь фигуры, состоящей из трапеций, высота каждой из которых равна h (рис 2). Если - остаточный член приближённой формулы (5), то

(6)

где

Формула парабол

Формула парабол (или формула Симпсона) имеет вид

(7)

(8)

Правая часть формулы (7) выражает площадь фигуры, составленной из параболических трапеций и т.д. (рис. 3). Дуга графика подынтегральной функции здесь заменена дугой параболы, проходящей через точки . Аналогичная замена произведена и для остальных дуг.

Для остаточного члена формулы (7) выполняется неравенство.

(9)

где

При переходе от формулы трапеции к формуле Симпсона точность вычисления интеграла (при фиксированном значении n ) возрастает столь значительно, потому что возрастает порядок аппроксимации подынтегральной функции интерполяционным многочленом: линейная аппроксимация сменяется на параболическую. При этом метод трапеции приводит, естественно, к точному значению интеграла, если линейна на каждом из отрезков , а метод Симпсона - если квадратична на каждом их этих отрезков. Выбора узлов на исходном отрезке с точки зрения теории произволен (на практике предпочитают использовать равностоящие узлы).

Существует, однако, иной связанный с именем Гаусса, подход к построению квадратурных формул, в котором центральное место играет выбор узлов для интерполирования подынтегральной функции. Ознакомится с этим подходом в его простейшей реализации.

Традиционно при получении квадратурных формул Гаусса в исходном интеграле выполняется замена переменной, переводящая интеграл по отрезку в интеграл по отрезку :

, или (10)

(11)

и можно далее, не теряя общности, развивать метод Гаусса применительно к интегралу вида .

Для разъяснения существа метода Гаусса обратимся к рис. Будем использовать простейшую (т.е. линейную) интерполяцию подынтегральной функции. Если в качестве узлов взять концы отрезка (так делалось при получении формулы трапеций), то различие в площадях криволинейной трапеции, ограниченной сверху прямой.

Вместо этого сформулируем задачу следующим образом: выбрать значения и так, чтобы площадь трапеции, ограниченной сверху прямой, проходящей через точки и , была равна интегралу от любого многочлена некоторой (наивысшей возможной) степени. Поскольку положение точек и определяют четыре координаты, то этот многочлен может определяться максимум четырьмя коэффициентами, т.е. являются многочленом 3-й степени

(12)

Легко установить, что уравнение прямой, проходящей через точки и , имеет вид

(13)

где

таким образом. Возникает следующая техническая задача: выбрать и так, чтобы равенство

(14)

имело место при любых значениях

Для её решения вычислим интегралы в (5):

Подставим в этом равенство и

Перегруппируем слагаемые в левой части равенства

Для того чтобы последнее равенство выполнялось при любых значениях необходимо и достаточно, чтобы

Отсюда следует одно из двух решений:

Отличающийся лишь нумерацией значений и .

И так, если взять узлами линейной интерполяции числа

(15)

то интеграл, вычисленный по формуле ,точно совпадает с интегралом от любого многочлена 3-й степени. Вычислив интеграл по указанной формуле с учётом (6), получим .

(16)

применима к любой (интегрируемой) функции и называется квадратной формулой Гаусса. Разумеется, для функции, не являются многочленом не старше 3-й степени, эта формула даёт лишь приближенное значение интеграла. Но интуитивно ясно, что это значение ближе к истинному, нежели то, которое даёт формула трапеций, также исходящая из интегрирования вспомогательной линейной функции вместо исходной.

Воспользовавшись формулой (11), можно для удобства использования записать формулу Гаусса применительно к исходному виду интеграла:

. (17)

Формулу доя оценки погрешности вычисления интеграла по методу Гаусса приведём без вывода:

; . (18)

Разумеется, для повышения точности вычисления интеграла по методу гаусса отрезок можно так же, как это делалось в методах трапеции и Симпсона, разделить на несколько частей и применять формулу (6) к каждому из них. Получим (при делении отрезка на равные части) практически используемые формулы для вычисления интеграла и оценки погрешности:

(19)

(20)

При практическом использовании формулы Гаусса (19) справедливы те же соображения. Которые привели к полуэмпирической оценке точности результата при двоичном счете.

Отметим, что формула (17) – лишь одна из семейства формул, называемых формулами гаусса для вычисления интегралов. Опираясь на изложенную ранее идею, можно строить квадратные формулы, точные для любого алгебраического многочлена любой нечестной степени.

При выполнении практической работы рассмотрите следующие примеры:

По формулам прямоугольников, приняв , вычислить .

В данном случае . С помощью формул (3) находим

По формулам (1) и (2) получаем

На сколько частей следует разбить промежуток интегрирования, чтобы с точностью 0,1 вычислить

Абсолютная погрешность при вычислении определённого интеграла по методу прямоугольников определяется формулой (4). Если ставится задача, чтобы , т.е. , то . В данном случае . Так как , . , то . Поскольку n – целое число, можно принять (для удобства вычислений можно взять , так как ).

Вычислить приближённо интеграл по формуле трапеций, приняв .

В данном случае по расчетной формуле , где , получаем . Так как , то . Находим значение

По формуле (5) получаем

На сколько частей нужно разбить промежуток интегрирования, чтобы по формуле трапеций вычислить интеграл с точностью

Для определения числа n отрезков, на которые нужно разбить промежуток интегрирования, воспользуемся формулой (6). Неравенство будет выполнено, если , откуда . Поскольку , то . Аналогично находим .

По формуле парабол вычислить , приняв .

По первой из формул (8) находим . Составляем таблицу значений (табл. 1). В последней строке этой таблицы стоят числа, равные суммам чисел, находящихся в соответствующих столбцах.

Читайте также: