Какое напряженное состояние называется чистым сдвигом как можно осуществлять явление чистого сдвига
Обновлено: 30.06.2024
Не подошло решение или нужна уникальная работа, оставляй бесплатную заявку и получай расчет на почту!
Чистый сдвиг и кручение
1. Чистый сдвиг и его особенности
2. Деформация при сдвиге
3. Определение напряжений при кручении стержней круглого поперечного сечения
4. Деформация и перемещения при кручении
5. Потенциальная энергия при упругих деформациях кручения
6. Кручение бруса с прямоугольным не круглым поперечным сечением
7. Статически неопределимые задачи на кручение
8. Кручение тонкостенного бруса замкнутого профиля
9. Стержни, работающие на кручение за пределами упругости
10. Мембранная аналогия при кручении
1. Чистый сдвиг и его особенности
Рассмотрим такое напряженное состояние, когда на гранях (на грани) выделенного элемента действуют только касательные напряжения . Такое напряженное состояние называют чистым сдвигом.
В качестве примера рассмотрим кручение тонкостенной цилиндрической трубы, нагруженной моментами, приложенными в торцевой плоскости.
бесконечно малый момент относительно оси Z
1 – бесконечно малая длина дуги, приходящаяся на выделенный элемент.
Величина касательных напряжений определяется из условий равновесия момента внутренних сил внешнему моменту.
– площадь, заключенная внутри срединной линии.
Рассмотрим напряжение при чистом сдвиге на наклонной площадке.
Проецируя все силы, действующие на призму ABC на оси n и t, из условия равновесия получили:
При касательные напряжения .
2. Деформация при сдвиге
Если на гранях выделенного элемента действуют только касательные напряжения, то в результате деформации прямоугольник превратится в параллелограмм.
Угол называется угловой деформацией или углом сдвига.
Многочисленные эксперименты показывают, что для многих материалов до известных пределов нагружения между напряжениями и деформациями имеет место линейная зависимость.
Это закон Гука при сдвиге.
G – модуль сдвига или модуль упругости II рода.
– Закон парности деформации сдвига:
При сдвиге угловые деформации двух взаимно перпендикулярных площадок равны по величине и противоположны по знаку.
3. Определение напряжений при кручении стержней круглого поперечного сечения
Стержень испытывает кручение, если в его поперечных сечениях возникают крутящие моменты, действующие в плоскости поперечного сечения.
Внутренние силовые факторы Т – крутящие моменты представляют собой равнодействующие внутренних сил. Фактически в поперечном сечении скручиваемого стержня действуют непрерывно распределённые внутренние касательные напряжения.
Можно показать, что при кручении справедлива гипотеза плоских жёстких сечений (Бернулли):
Сечения после деформации остаются плоскими и нормальными к оси стержня.
Построение эпюр (ДЗ).
Задача является актуальной для валопроводов, трансмиссий.
В выделенном сечении при кручении действует Т(Z) и вызывает возникновение касательных напряжений и эти напряжения распределены непрерывно по поперечному сечению.
– максимальная угловая деформация сдвига на поверхности стержня поперечного сечения.
– бесконечно малый угол закручивания вала длиной dZ.
Выразим длину дуги 2 – 2′ через и , считая достаточно малым.
– постоянная для фиксированного сечения.
Исследуем закон Гука для деформации сдвига и перейдем к напряжениям (касательным).
чем больше , тем больше .
При кручении деформации сдвига и касательные напряжения прямопропорциональны расстоянию от центра тяжести сечения.
Крутящий момент в сечении представляет собой равнодействующий момент касательных напряжений в сечении.
В [3] неизвестна, и для ее определения воспользуемся уравнением равновесия в моментах относительно оси Z.
Введем бесконечно малую площадку dA, подставив сюда выражение для касательных напряжений.
Gip – жесткость стержня при кручении.
4. Деформации и перемещения при кручении
Для вычисления деформаций вала при кручении воспользуемся формулой:
– относительный угол закручивания участка стержня длинною dZ
Если GIp = const , то Перемещение —
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания. Этот угол равен:
Для обеспечения требуемой жесткости вала при кручении необходимо ограничить наибольший относительный угол закручивания.
5. Потенциальная энергия при упругих деформациях кручения
При кручении внешние моменты совершают работу вследствие поворота сечений, к которым они приложены. Эта работа расходуется на создание запаса потенциальной энергии деформации, численно равной работе внутренних сил.
Аналогично тому как это было сделано при растяжении пружин, эта работа ровна половине произведения конечного значения момента на окончательный угол закручивания:
Элементарная работа внутренних сил
Уравнение [4] представим в виде
После подстановки и интегрирования
Если учесть, что на практике в расчёте валов GIp = const, T = const для всего вала или отдельных участков
Энергетические методы получают все больше в проектировании конструкций (принцип энергии системы).
1) Пусть в некоторой текущей точке
2) Т(z) – действует при кручении Z
3) Бесконечно малый участок dZ
5) Бесконечно малая энергия, затрачиваемая на деформирование выделенного участка. Потенциальная энергия упругой деформации dU
Теорема Клапейрона для определения работы упруго деформированного тела.
6. Кручение бруса с прямоугольным не круглым поперечным сечением
Определение напряжений в брусе с некруглым поперечным сечением представляет собой довольно сложную задачу, которая не может быть решена методом сопротивления материалов. Причина заключается в том, что для некруглого сечения упрощающая гипотеза неизменности плоских сечений (гипотеза Бернулли) оказывается неприемлемой. Сечения существенно искривляются, в результате чего изменится картина распределения напряжений по сечению.
Задача, кроме того, усложняется тем, что для некруглого сечения напряжения должны определяться уже функцией двух переменных x и y.
Выскажем общие соображения относительно законов распределения напряжений в поперечных сечениях не круговой формы, а затем приведём готовые формулы, полученные методами теории упругости.
1. Касательные напряжения для точек поперечного сечения, расположенных на контуре, обязательно направлены по касательной к внешнему контуру.
Гипотеза Бернулли не может быть использована. Решение может быть получено с помощью трехмерной теории упругости.
Касательное напряжение в точках, расположенных на контурах сечений, действует в направлении вдоль контура.
1. Момент, передаваемый валом
2. Расчет вала из условий прочности
3. Расчет вала из условий жесткости
7. Статически неопределимые задачи на кручение
При кручении, так же как и при растяжении, встречаются задачи, решение которых не может быть получено с помощью одних только уравнений равновесия. Число неизвестных в таких задачах превышает число уравнений равновесия. Порядок решения таких задач тот же самый, что и при решении статически неопределимых задач на растяжение – сжатие.
брус стержень деформация кручение
Отсюда определяем TA и подставляем в [1] для определения TB
8. Кручение тонкостенного бруса замкнутого профиля.
Значительно более жесткими и поэтому более целесообразными при кручении являются тонкостенные стержни замкнутого профиля.
Рассмотрим цилиндрический стержень, поперечное сечение которого имеет достаточно общую форму.
t – меняется достаточно медленно
Геометрическое место точек, равноотстоящих от внешнего и внутреннего контуров поперечного сечения, называются средней линией сечения.

Однородный чистый сдвиг можно получить нагружением пластины, захваченной в жесткие контурные шарнирно соединенные накладки (рис.8.1 а).
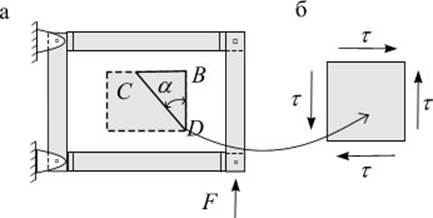
Для всех точек пластины касательные напряжения будут равны
где – сдвигающая сила; – площадь сечения пластины; а касательные напряжения принимаем равномерно распределенными по сечению. На гранях выделенного прямоугольного элемента возникают только касательные напряжения (рис. 8.1 б).
Такое напряженное состояние называется чистым сдвигом.
Посмотрим, как при чистом сдвиге изменяются напряжения в зависимости от ориентации секущих площадок. Выделим трехгранную призму DCB (рис.8.1) и рассмотрим ее в равновесии (рис. 8.2).
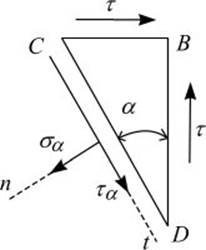
На грани DС возникают как касательные, так и нормальные напряжения. Проецируем все силы, действующие на элемент, на оси n и t.
где и , получаем
При = 0 и = 90 0 напряжения = 0, =t. При = ± 45 0 напряжения = 0, = ±t. Следовательно, на гранях элемента, повернутого на 45 0 , будут обнаружены только нормальные напряжения, причем на одной паре граней они растягивающие, на другой - сжимающие (рис. 8.3).
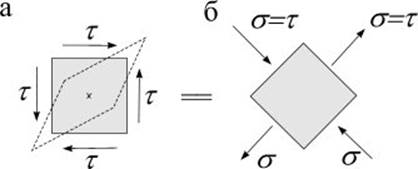
Чистый сдвиг может быть представлен как одновременное растяжение и сжатие по двум взаимно перпендикулярным направлениям.
8.1.2. Закон Гука при чистом сдвиге
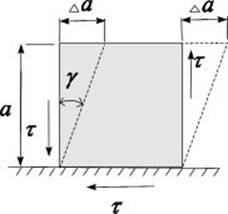
Малый угол , на который изменяется первоначально прямой угол, называется углом сдвигаилиотносительным сдвигом. Величину абсолютного смещения грани называют абсолютным сдвигом.
Учитывая малость , можно записать:
Деформация сдвига характеризуется изменением углов элемента, длина ребер не меняется (рис. 8.3 а).
Из опытов на кручение трубчатых образцов из пластичной стали получают диаграмму сдвига в координатах (рис. 8.5). В пределах упругих деформаций справедлива линейная зависимость: закона Гука при сдвиге
где – модуль упругости материала при сдвиге (Па). Для стали = 8×10 4 МПа.
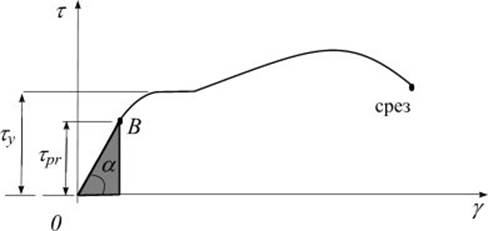
Для изотропного материала между , и , характеризующими упругие свойства, существует зависимость
Перепишем (8.4) с учетом (8.5) и (8.2), получим закон Гука для абсолютного сдвига:
где – жесткость бруса при сдвиге.
8.1.3. Потенциальная энергия при чистом сдвиге
Потенциальная энергия деформации рассматриваемого элемента равна работе касательных (сдвигающих) сил, приложенных к граням элемента:
Объем элемента V, поэтому удельная потенциальная энергия:
, или с учетом (8.2)
причем численно она равна площади треугольника на диаграмме сдвига (рис.8.5).
8.1.4. Понятие о срезе и смятии
Срезом называют такой вид нагружения бруса, при котором в поперечном сечении возникает только поперечная сила Q.
Деформация среза имеет место при действии на брус с противоположных сторон двух равных сил на близком расстоянии друг от друга (рис. 8.6 а).
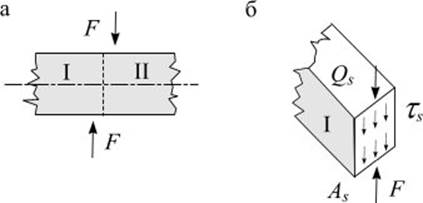
Примером такого действия сил на брус может быть разрезание ножницами прутьев, полосы и т.п.
Рассмотрим отсеченную часть I в равновесии (рис. 8.6 б), очевидно
Принимая равномерно распределенными по площади сечения , будем иметь , и условие прочности на срез принимает вид
где – срезающая сила; – площадь среза; – расчетное сопротивление материала срезу.
Расчет на срез во многих случаях сопровождается расчетом на смятие.
Смятие - это пластическая деформация, возникающая на поверхностях контакта.
Читайте также:
- Как обжаловать постановление комиссии по делам несовершеннолетних
- Горбунова л и язык как знаковая система особого рода учеб пособие 2013
- Нужен ли загранпаспорт в таджикистан если двойное гражданство
- Для чего необходимо предвыборная агитация для предоставления избирателям информации
- Как и кем оформляется решение о назначении переводчика

