Как правильно оформить решение системы уравнений с двумя переменными

Обновлено: 18.05.2024

Пример:
Пара значений \(x=3\);\(y=-1\) является решением первой системы, потому что при подстановке этих тройки и минус единицы в вместо \(x\) и \(y\), оба уравнения превратятся в верные равенства \(\begin3-2\cdot (-1)=5 \\3 \cdot 3+2 \cdot (-1)=7 \end\)

Отметим, что такие пары часто записывают короче: вместо "\(x=3\); \(y=-1\)" пишут так: \((3;-1)\).

Как решить систему линейных уравнений?

Есть три основных способа решения систем линейных уравнений:

Возьмите любое из уравнений системы и выразите из него любую переменную.

Полученное выражение подставьте вместо этой переменной в другое линейное уравнение системы.

Ответ запишите парой чисел \((x_0;y_0)\)

Замечание к шагу 1: нет никакой разницы какую переменную и из какого уравнения выражать. Обычно более удобно выражать ту переменную, перед которой нет коэффициента или, говоря точнее, коэффициент которой равен единице (в примере выше это был икс в первом уравнении).

Почему так? Потому что во всех остальных случаях у нас при выражении переменной получилась бы дробное выражение . Попробуем, например, выразить икс из второго уравнения системы:

И сейчас нам нужно будет эту дробь подставлять в первое уравнение и решать то, что получиться. До верного ответа мы бы всё равно дошли, но идти было бы неудобнее

Равносильно преобразовывая каждое уравнение в отдельности, запишите систему в виде:\(\begina_1 x+b_1 y=c_1\\a_2 x+b_2 y=c_2\end\).

Теперь нужно сделать так, чтоб коэффициенты при одном из неизвестных стали одинаковы (например, (\(3\) и \(3\)) или противоположны по значению (например, \(5\) и \(-5\)). В нашем примере уравняем коэффициенты при игреках. Для этого первое уравнение домножим на \(2\), а второе - на \(3\).

\(\begin2x+3y=13 |\cdot 2\\ 5x+2y=5 |\cdot 3\end\)\(\Leftrightarrow\)\(\begin4x+6y=26\\15x+6y=15\end\)\(\Leftrightarrow\)

Сложите (или вычтите) почленно обе части уравнения так, чтобы получилось уравнение с одним неизвестным.

Ответ запишите парой чисел \((x_0;y_0)\).

Пример. Решите систему уравнений: \(\begin12x-7y=2\\5y=4x-6\end\)

Приводим систему к виду \(\begina_1 x+b_1 y=c_1\\a_2 x+b_2 y=c_2\end\) преобразовывая второе уравнение.

Знаки при иксах разные, поэтому чтоб иксы пропали, уравнения надо сложить.

Делим уравнение на \(8\), чтобы найти \(y\).

Игрек нашли. Теперь найдем \(x\), подставив вместо игрека \(-2\) в любое из уравнений системы.

Икс тоже найден. Пишем ответ.

Приведите каждое уравнение к виду линейной функции \(y=kx+b\).

Постройте графики этих функций. Как? Можете прочитать здесь .

Матхак. Если сомневаетесь в правильности ответа (неважно каким способом вы решали), проверьте подстановкой значений \(x_0\) и \(y_0\) в каждое уравнение. Если оба уравнения превратятся в верные равенства, то ответ правильный.
Пример: решая систему \(\begin3x-8=2y\\x+y=6\end\), мы получили ответ \((4;2)\). Проверим его, подставив вместо икса \(4\), а вместо игрека \(2\).

Оба уравнения сошлись, решение системы найдено верно.

Пример. Решите систему уравнений: \(\begin3(5x+3y)-6=2x+11\\4x-15=11-2(4x-y)\end\)

Перенесем все выражения с буквами в одну сторону, а числа в другую.

Во втором уравнении каждое слагаемое - четное, поэтому упрощаем уравнение, деля его на \(2\).

Эту систему линейных уравнений можно решить любым из способов, но мне кажется, что способ подстановки здесь удобнее всего. Выразим y из второго уравнения.

Подставим \(6x-13\) вместо \(y\) в первое уравнение.

Первое уравнение превратилась в обычное линейное . Решаем его.

Сначала раскроем скобки.

Перенесем \(117\) вправо и приведем подобные слагаемые.

Поделим обе части первого уравнения на \(67\).

Ура, мы нашли \(x\)! Подставим его значение во второе уравнение и найдем \(y\).

Статья знакомит с таким понятием, как определение системы уравнений и ее решением. Будут рассмотрены часто встречающиеся случаи решений систем. Приведенные примеры помогут подробно пояснить решение.

Определение системы уравнений

Чтобы перейти к определению системы уравнений, необходимо обратить внимание на два момента: вид записи и ее смысл. Чтобы понять это, нужно подробно остановиться на каждом из видов, тогда сможем прийти к определению систем уравнений.

Например, возьмем два уравнения 2 · x + y = − 3 и x = 5 , после чего объединим фигурной скобкой такого плана:

2 · x + y = - 3 , x = 5 .

Уравнения, объединенные фигурной скобкой, считаются записями систем уравнений. Они задают множества решений уравнений данной системы. Каждое решение должно являться решением всех заданных уравнений.

Другими словами это означает, что любые решения первого уравнения будут решениями всех уравнений, объединенных системой.

Системы уравнений – это некоторое количество уравнений, объединенных фигурной скобкой, имеющих множество решений уравнений, которые одновременно являются решениями для всей системы.

Основные виды систем уравнений

Видов уравнений достаточно много, как систем уравнений. Для того, чтобы было удобно решать и изучать их, подразделяют на группы по определенным характеристикам. Это поможет в рассмотрении систем уравнений отдельных видов.

Для начала уравнения классифицируются по количеству уравнений. Если уравнение одно, то оно является обычным уравнением, если их более, тогда имеем дело с системой, состоящей из двух или более уравнений.

Другая классификация затрагивает число переменных. Когда количество переменных 1 , говорят, что имеем дело с системой уравнений с одной неизвестной, когда 2 – с двумя переменными. Рассмотрим пример

x + y = 5 , 2 · x - 3 · y = 1

Очевидно, что система уравнений включает в себя две переменные х и у .

При записи таких уравнений считается число всех переменных, имеющихся в записи. Их наличие в каждом уравнении необязательно. Хотя бы одно уравнение должно иметь одну переменную. Рассмотрим пример системы уравнений

2 x = 11 , x - 3 · z 2 = 0 , 2 7 · x + y - z = - 3

Данная система имеет 3 переменные х , у , z . Первое уравнение имеет явный х и неявные у и z . Неявные переменные – это переменные, имеющие 0 в коэффициенте. Второе уравнение имеет х и z , а у неявная переменная. Иначе это можно записать таким образом

2 x + 0 · y + 0 · z = 11

А другое уравнение x + 0 · y − 3 · z = 0 .

Третья классификация уравнений – это вид. В школе проходят простые уравнения и системы уравнений, начиная с систем двух линейных уравнений с двумя переменными. Имеется в виду, что система включает в себя 2 линейных уравнения. Для примера рассмотрим

2 · x - y = 1 , x + 2 · y = - 1 и - 3 · x + y = 0 . 5 , x + 2 2 3 · y = 0

Это основные простейшие линейные уравнения. Далее можно столкнуться с системами, содержащими 3 и более неизвестных.

В 9 классе решают уравнения с двумя переменными и нелинейные. В целых уравнениях повышается степень для увеличения сложности. Такие системы называют системами нелинейных уравнений с определенным количеством уравнений и неизвестных. Рассмотрим примеры таких систем

x 2 - 4 · x · y = 1 , x - y = 2 и x = y 3 x · y = - 5

Обе системы с двумя переменными и обе являются нелинейными.

При решении можно встретить дробно-рациональные уравнения. Например

x + y = 3 , 1 x + 1 y = 2 5

Могут называть просто системой уравнений без уточнения, каких именно. Редко уточняют сам вид системы.

Старшие классы переходят к изучению иррациональных, тригонометрических и показательных уравнений. Например,

x + y - x · y = 5 , 2 · x · y = 3 , x + y = 5 · π 2 , sin x + cos 2 y = - 1 , y - log 3 x = 1 , x y = 3 12 .

Высшие учебные заведения изучают и исследуют решения систем линейных алгебраических уравнений (СЛАУ). Левая часть таких уравнений содержит многочлены с первой степенью, а правая – некоторые числа. Отличие от школьных в том, что количество переменных и количество уравнений может быть произвольным, чаще всего несовпадающим.

Решение систем уравнений

Решение системы уравнений с двумя переменными – это пара переменных, которая при подстановке обращает каждое уравнение в верное числовое неравенство, то есть является решением для каждого уравнения данной системы.

К примеру, пара значений х = 5 и у = 2 являются решением системы уравнений x + y = 7 , x - y = 3 . Потому как при подстановке уравнения обращаются в верные числовые неравенства 5 + 2 = 7 и 5 − 2 = 3 . Если подставить пару х = 3 и у = 0 , тогда система не будет решена, так как подстановка не даст верное уравнение, а именно, мы получим 3 + 0 = 7 .

Сформулируем определение для систем, содержащих одну и более переменных.

Решение системы уравнений с одной переменной – это значение переменной, которая является корнем уравнений системы, значит, все уравнения будут обращены в верные числовые равенства.

Рассмотрим на примере системы уравнений с одной переменной t

t 2 = 4 , 5 · ( t + 2 ) = 0

Число - 2 – решение уравнения, так как ( − 2 ) · 2 = 4 , и 5 · ( − 2 + 2 ) = 0 являются верными числовыми равенствами. При t = 1 система не решена, так как при подстановке получим два неверных равенства 12 = 4 и 5 · ( 1 + 2 ) = 0 .

Решение системы с тремя и более переменными называют тройку, четверку и далее значений соответственно, которые обращают все уравнения системы в верные равенства.

Если имеем значения переменных х = 1 , у = 2 , z = 0 , то подставив их в систему уравнений 2 · x = 2 , 5 · y = 10 , x + y + z = 3 , получим 2 · 1 = 2 , 5 · 2 = 10 и 1 + 2 + 0 = 3 . Значит, эти числовые неравенства верные. А значения ( 1 , 0 , 5 ) не будут решением, так как, подставив значения, второе из них будет неверное, как и третье: 5 · 0 = 10 , 1 + 0 + 5 = 3 .

Системы уравнений могут не иметь решений вовсе или иметь бесконечное множество. В этом можно убедиться при углубленном изучении данной тематики. Можно прийти к выводу, что системы уравнений – это пересечение множеств решений всех ее уравнений. Раскроем несколько определений:

Несовместной называют систему уравнений, когда она не имеет решений, в противном случае ее называют совместной.

Неопределенной называют систему, когда она имеет бесконечное множество решений, а определенной при конечном числе решений либо при их отсутствии.

Такие термины редко применяются в школе, так как рассчитаны для программ высших учебных заведений. Знакомство с равносильными системами углубит имеющиеся знания по решению систем уравнений.

Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:

	x - 4y = 2
	3x - 2y = 16

Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.

Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.

Способ подстановки

Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.

Рассмотрим решение системы уравнений:

	x - 4y = 2
	3x - 2y = 16

Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:

x - 4y = 2;

x = 2 + 4y .

Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:

3x	- 2y = 16;
3( 2 + 4y )	- 2y = 16.

Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.

3(2 + 4y) - 2y = 16;

6 + 12y - 2y = 16;

6 + 10y = 16;

10y = 16 - 6;

10y = 10;

y = 10 : 10;

y = 1.

Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:

x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.

Ответ: x = 6, y = 1.

Способ сравнения

Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.

Например, для решение системы:

	x - 4y = 2
	3x - 2y = 16

найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):

x - 4y = 2	3x - 2y = 16
-4y = 2 - x	-2y = 16 - 3x
y = (2 - x) : - 4	y = (16 - 3x) : -2

Составляем из полученных выражений уравнение:

2 - x	=	16 - 3x
-4	=	-2

Решаем уравнение, чтобы узнать значение x:

Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:

x - 4y = 2	3x - 2y = 16
6 - 4y = 2	3 · 6 - 2y = 16
-4y = 2 - 6	-2y = 16 - 18
-4y = -4	-2y = -2
y = 1	y = 1

Ответ: x = 6, y = 1.

Способ сложения или вычитания

Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.

	x - 4y = 2
	3x - 2y = 16

Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:

(3x - 2y) · -2 = 16 · -2

-6x + 4y = -32

	x - 4y = 2
	-6x + 4y = -32

Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:

+	x - 4y = 2
+	-6x + 4y = -32
-5x = -30

Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.

Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.

Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:

3x - 12y = 6

	3x - 12y = 6
	3x - 2y = 16

Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:

-	3x - 12y = 6
-	3x - 2y = 16
-10y = -10

Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:

3x - 2y = 16

3x - 2 · 1 = 16

3x - 2 = 16

3x = 16 + 2

3x = 18

x = 18 : 3

x = 6

Ответ: x = 6, y = 1.

Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:

Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.

в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

Теоретический материал для самостоятельного изучения.

Решение систем двух линейных уравнений с двумя неизвестными.

Пусть дана система двух линейных уравнений с двумя неизвестными.

Перенеся все члены правых частей этих уравнений в левые части, и приведя подобные члены, получим равносильную данной систему вида:

где ─ некоторые числа.

Мы уже знаем, как решать такую систему, когда все коэффициенты при неизвестных отличны от нуля. Мы знаем так же, что если коэффициенты при неизвестных непропорциональны, то решение системы существует и единственно; если же коэффициенты при неизвестных системы пропорциональны, то либо решений бесконечно много, либо нет ни одного решения.

Нам остаётся рассмотреть те случаи, когда некоторые коэффициенты при неизвестных равны нулю. Рассмотрим это на характерных примерах.

Пример 1. Решим систему уравнений:

Второе уравнение этой системы имеет отличные от нуля коэффициенты при неизвестных, а первое уравнение имеет коэффициент при , отличный от нуля, и коэффициент при , равный нулю.

Эту систему проще решить методом подстановки. Найдем из первого уравнения:

И подставим его во второе. Получим:

Таким образом, пара чисел есть единственное решение системы.

Пример 2. Решим систему уравнений:

Система есть частный случай системы , где

Единственным решением этой системы является пара чисел

Пример 3. Решим систему уравнений:

Из каждого уравнения системы получим

Так как систему мы рассматриваем как частный случай системы , где то система может быть записана так:

Здесь может быть любым числом, а .

Таким образом, решения системы записываются в виде пар чисел , где ─ любое число.

Пример 4. Решим систему уравнений

Эта система противоречива (не имеет решений), потому что не может одновременно равняться и 1, и .

Пример 5. Решим систему уравнений:

Если , то эта система противоречива, потому что никакая пара чисел не удовлетворяет второму уравнению системы

Если , то второе уравнение обращается в верное равенство при любых Остаётся только первое уравнение. Оно уже рассматривалось. Следовательно, все решения первого уравнения являются решениями системы.

О количестве решений системы двух уравнений первой степени с двумя неизвестными.

Пусть дана система уравнений:

где все коэффициенты отличны от нуля.

а) имеет единственное решение, если ;

б) не имеет решений, если ;

в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.

Доказательство.

Из первого уравнения системы получим, что:

. Подставив полученное выражение вместо во второе уравнение системы и учитывая, что получим уравнение:

Здесь возможны три случая.

то уравнение имеет единственный корень, поэтому и система имеет единственное решение.

Так как и то условие можно записать в виде

то уравнение не имеет корней и система не имеет решений.

Так как то условия можно записать в виде

то уравнение имеет бесконечно много корней, поэтому и система имеет бесконечно много решений.

Так как то условия можно записать в виде

если то система имеет единственное решение;

если то система не имеет решений;

если то система имеет бесконечно много решений, и эти решения задаются парами , где любое число.

Теорема доказана.

Пример 1. Определим число решений системы уравнений:

а) Так как выполняется условие , то система имеет единственное решение.

б) Так как выполняется условие , то система имеет бесконечно много решений.

в) Так как выполняется условие то система не имеет решений.

Ответ: а) единственное решение; б) бесконечно много решений; в) нет решений.

Пример 2. При каком значении система

не имеет решений?

Система не имеет решений, если выполняется условие

. Условие выполняется лишь при При этом условие также выполняется. Следовательно, система не имеет решений при

Пример 3. Существует ли значение , при котором система не имеет решений?

Система не имеет решений, если выполняется условие . Условие выполняется лишь при При этом условие не выполняется. Следовательно, таких не существует.

Ответ: не существует.

Разбор решения заданий тренировочного модуля.

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Впишите пропущенные элементы при решении системы.

Перенесем из первого уравнения в правую часть 4, получим

Найдем отношение коэффициентов при х и у в системе:

‑ так как отношения __ равны, значит, система имеет одно решение. Решим систему способом подстановки:

Перенесем из первого уравнения в левую часть 4, получим:

Найдем отношение коэффициентов при х и у в системе:

‑ так как отношения не равны, значит, система имеет одно решение. Решим систему способом подстановки:

№2. Тип задания: восстановление последовательности элементов горизонтальное / вертикальное.

В начале урока предлагаем рассмотреть задачу, решая которую мы показываем, что же такое система уравнений, что представляет собой решение системы. Затем мы знакомимся с одним из способов решения систем. И рассматриваем примеры.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока "Системы линейных уравнений с двумя переменными"

· рассмотреть графический способ решения систем линейных уравнений.

Прежде, чем приступить к рассмотрению новой темы вспомним, что:

А теперь давайте рассмотрим задачу. Сумма двух чисел равна 25, а их разность – 17. Чему равны эти числа?

Пусть икс – первое число, а игрек – второе.

Так как по условию задачи сумма этих чисел равна 25, то можно составить уравнение:

Также известно, что разность чисел равна 17, а тогда можем записать следующее уравнение:

Таким образом, мы получили два уравнения с двумя переменными.

Чтобы ответить на вопрос задачи, нам надо найти такие значения переменных x и y, которые обращают каждое из уравнений в верное равенство, то есть найти общие решения уравнений.

Говорят, что требуется решить систему уравнений и записывают вот таким образом:

Теперь подбором найдём пару значений переменных:

Действительно, эта пара является решением каждого уравнения системы, так при подстановке этих значений мы получаем верные равенства.

Такая пара чисел называется решением системы.

Определение.

Решением системы уравнений с двумя переменными называется пара значений переменных, которая обращает каждое уравнение системы в верное равенство.

Решить систему уравнений – значит найти все её решения или доказать, что их нет.

Существует несколько способов решения систем уравнений с двумя переменными. И сейчас мы познакомимся с одним из них.

Возьмём следующую систему

Вам уже известно, как строить график линейного уравнения с двумя переменными. Давайте построим график каждого уравнения нашей системы.

Из каждого уравнения системы выразим переменную у через переменную х.

Так как графиком каждого из уравнений будет прямая, то для его построения нам достаточно указать две точки.

Отметим эти точки на координатной плоскости и проведём через них линии.

Обратите внимание, что построенные графики пересекаются в точке:

Координаты этой точки удовлетворяют обоим уравнениям, то есть являются решением системы уравнений. В этом можете убедиться самостоятельно, подставив эти значения в уравнения системы.

Таким образом, система имеет единственное решение:

Такой способ решения системы называется графическим.

Возникает вопрос: всегда ли система уравнений с двумя переменными имеет решения и если имеет, то сколько?

На примере мы с вами увидели, что если прямые (то есть графики уравнений) пересекаются, то система имеет единственное решение. А вот если прямые параллельны, то система не имеет решений. Если же прямые совпадают, то система имеет бесконечно много решений.

Рассмотрим пример, в котором надо выяснить, сколько решений имеет система.

Но сначала вспомним, что:

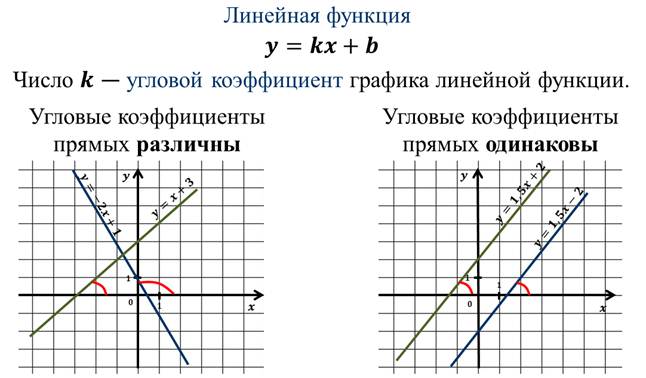
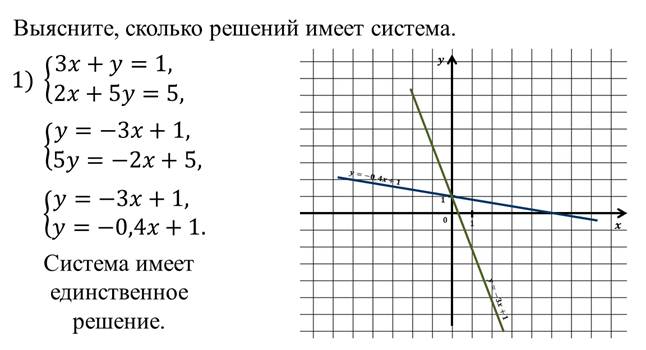
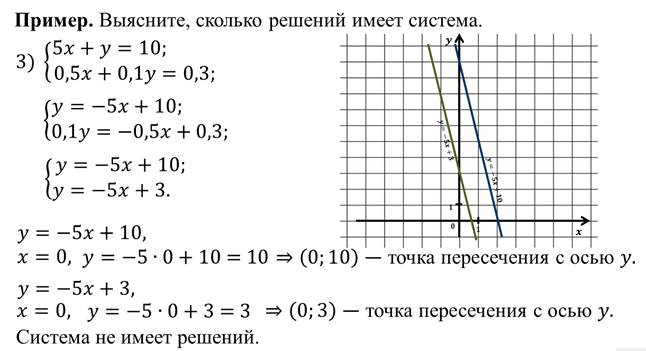
Итак, сегодня на уроке мы рассмотрели одни из способов решения систем линейных уравнений с двумя переменными. Но следует отметить, что графический способ позволяет чаще всего находить решения лишь приближённо.

Читайте также: