Что значит знак в геометрии дуга в право

Обновлено: 19.05.2024

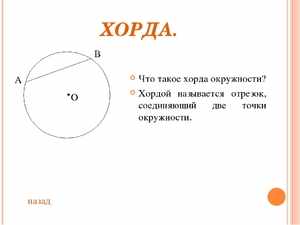
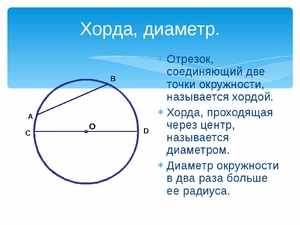
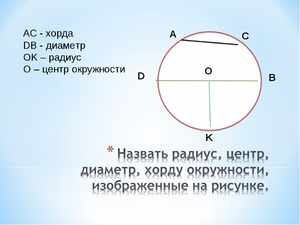
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.

Как построить геометрическую хорду

Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.

Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.

Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.

Свойства

Существует ряд закономерностей, связывающих между собой хорды и центр круга:

Взаимосвязь с радиусом и диаметром

Вышеуказанные математические понятия связаны между собой следующими закономерностями:

Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.

Хорда и радиус

Между этими понятиями существуют следующие связи:

Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.

Отношения со вписанными углами

Углы, вписанные в окружность, подчиняются следующим правилам:

Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
Вписанный угол, который опирается на диаметр круга, является прямым.
Равные между собой по размеру отрезки стягивают равные центральные углы.
Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.

Взаимодействия с дугой

Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:

Две равные между собой хорды стягивают равные дуги.
Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.

Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

А, В, С, D, . , L, М, N, .

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

а, b, с, d, . , l, m, n, .

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

β(d₁ d₂gα) — поверхность β определяется направляющими d₁ и d₂ , образующей g и плоскостью параллелизма α.

5. Углы обозначаются:

∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, . , ∠φ°, .

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

8. Для плоскостей проекций приняты обозначения: π₁ и π₂, где π₁ - горизонтальная плоскость проекций;

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

9. Оси проекций обозначаются: х, у, z, где х - ось абсцисс; у - ось ординат; z - ось аппликат.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

А', В', С', D', . , L', М', N', горизонтальные проекции точек; А", В", С", D", . , L", М", N", . фронтальные проекции точек; a' , b' , c' , d' , . , l', m' , n' , — горизонтальные проекции линий; а" ,b" , с" , d" , . , l" , m" , n" , . фронтальные проекции линий; α', β', γ', δ'. ζ',η',ν'. горизонтальные проекции поверхностей; α", β", γ", δ". ζ",η",ν". фронтальные проекции поверхностей.

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

Так: h_0α - горизонтальный след плоскости (поверхности) α;

f_0α - фронтальный след плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3. n:

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

А 0 , В 0 , С 0 , D 0 , .

1 0 , 2 0 , 3 0 , 4 0 , .

a 0 , b 0 , c 0 , d 0 , .

α 0 , β 0 , γ 0 , δ 0 , .

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

А 1 0 , В 1 0 , С 1 0 , D 1 0 , .

1 1 0 , 2 1 0 , 3 1 0 , 4 1 0 , .

a 1 0 , b 1 0 , c 1 0 , d 1 0 , .

α 1 0 , β 1 0 , γ 1 0 , δ 1 0 , .

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Множество дуга , или параметрические кривой в векторном пространстве Е конечной размерности данные из интервала I , который изменяется в параметре , а функция I в Е .

Поскольку любое аффинное пространство естественным образом связано с векторным пространством, понятие геометрической дуги или параметризованной дуги также существует в аффинной геометрии и рассматривается путем естественного связывания M ( t ) и вектор-функции . ж ( т ) знак равно О M ( т ) → >>

Резюме

Определение

Параметризованная дуга классов в векторном пространстве E конечной размерности - это заданная ПРОТИВ k > ^ >

интервал I , где действительный параметр т будет изменяться
из функции F от I до Е , класса ПРОТИВ k > ^ >

В данных эталонных Е , функция F имеет компоненты х ( т ), у ( т ), . . Например, вот настройка единичной окружности плоскости (пройденной бесконечное количество раз):

На практике функция f может иметь для области определения объединение непересекающихся интервалов; Затем мы изучим отдельно каждую из соответствующих ветвей кривой (см. связность ).

В дифференциальной геометрии не рассматриваются только непрерывные дуги . Пример кривой Пеано показывает, что их поведение может быть очень сложным.

Точка параметра и геометрическая точка, кратность

точка параметра f , выражение, которое обозначает совместные данные t и точки f ( t ) ;
геометрическая соответствующая точка , которая является точкой Е .

Таким образом, в случае нескольких точек две или более различных точек параметров совпадают с одной и той же геометрической точкой. Можно говорить о двойной или тройной точке или о кратности k, если известно точное количество значений параметра, которые дают эту геометрическую точку. Если дуга не имеет кратной точки ( инъективная f ), она называется простой .

В частном случае, когда функция периодическая , мы говорим, что кривая замкнута . Затем мы предпочтем изучать его за период и говорить о множественности точек относительно периода. Таким образом , лемниската Бернулли:

< Икс ( т ) знак равно грех ⁡ т 1 + потому что 2 ⁡ т у ( т ) знак равно грех ⁡ т потому что ⁡ т 1 + потому что 2 ⁡ т x (t) = t>> \\ y (t) = t>> \ end >>

замкнуто ( 2π -периодично) и допускает начало координат для двойной точки ( t = 0 или π ). В замкнутые кривые ряд интересных свойств , описанных в статье.

Изменение параметра

Рассмотрим класс дугу в виде интервала I и функцию ф из I в Е . Траектория называется множество е ( I ) геометрических точек. Но одну и ту же траекторию можно пройти разными способами. ПРОТИВ k > ^ >

Итак, если u = φ ( t ) является функцией интервала J в классе I , то это тоже дуга . Чтобы пройти по той же траектории и пройти одинаковое количество раз в одни и те же точки в одном порядке, нужно наложить, что φ - строго монотонная биекция. ПРОТИВ k > ^ > грамм знак равно ж ∘ φ ПРОТИВ k > ^ >

На самом деле, больше необходимо: обеспечить совместимость с дифференциальным исчислением, мы будем говорить , что г является допустимой параметризацией дуги , если φ является - диффеоморфизм . Две дуги до и после повторной параметризации считаются эквивалентными . Мы называем геометрической дугой любой класс эквивалентности этого отношения. ПРОТИВ k > ^ > ПРОТИВ k > ^ >

Повторяя изменение настройки параметра , можно записать формулу вывода составных функций, соединяющих векторы, полученные из двух дуг, в двух соответствующих точках. грамм знак равно ж ∘ φ

Т ж знак равно ж ′ ( ты 0 ) Т грамм знак равно грамм ′ ( т 0 ) знак равно φ ′ ( т 0 ) ж ′ ( φ ( т 0 ) ) = f '(u_ ) \ qquad T_ = g' (t_ ) = \ varphi '(t_ ) f' (\ varphi (t_ >))>

Два производных вектора коллинеарны с ненулевым отношением коллинеарности

Примеры инвариантов

Некоторые концепции не меняются при изменении настроек

траектория: все точки совпадают
понятие регулярной точки (вектор ненулевой производной): две соответствующие точки являются обеими регулярными или обеими точками остановки (производные компенсируют друг друга).
понятие касательной (как предел секущих ), которое совместимо с предыдущим свойством
длина дуги между двумя точками, с одной стороны, и два соответствующих точками, с другой стороны.

Следовательно, мы будем говорить, что эти понятия распространяются на геометрическую дугу.

Но некоторые свойства включают ориентацию дуги, то есть направление движения. В этом случае следует различать два типа изменения параметров.

то есть имеет строго положительную производную в любой точке, и говорят, что она сохраняет ориентацию. φ
либо имеет строго отрицательную производную в любой точке, и мы говорим, что она меняет ориентацию. φ

В первом случае (с учетом ориентации) смена параметризации сохраняет другие понятия

Мы можем определить понятие ориентированной геометрической дуги , ограничившись изменениями настроек с учетом ориентации.

Параметризация полярным углом

Мы помещаемся в ориентированную евклидову плоскость, возвращенную в ортонормированную систему координат . Частый способ определения кривых - дать их полярному уравнению r функцию от θ : r = h ( θ ) . Это частный случай параметризованной дуги, поскольку мы можем записать x ( θ ) = h ( θ ) cos ( θ ), y ( θ ) = h ( θ ) sin ( θ ) .

Мы можем спросить себя, при каких условиях для данной дуги мы можем найти такое полярное уравнение . Нам нравится иметь дело со случаем дуг, которые не проходят через саму точку O , потому что это создает дополнительные трудности.

Если ( я , е ) определяет дугу , которая никогда не проходит через O , то есть функции г и θ , также , что при всех т , ф ( т ) имеет полярные координаты г ( т ) и θ ( т ) . ПРОТИВ k > ^ > ПРОТИВ k > ^ >

Это демонстрируется применением теоремы о подъеме .

При тех же предположениях, если функция θ является диффеоморфизмом, мы можем взять θ в качестве параметра и, таким образом, получить истинное полярное уравнение.

Читайте также: